| Codeforces Round 626 (Div. 2, по задачам Открытой олимпиады школьников по программированию) |
|---|
| Закончено |
Дан массив $$$a$$$ длины $$$n$$$ и массив $$$b$$$ длины $$$m$$$, оба состоящие из чисел $$$0$$$ и $$$1$$$. Рассмотрим матрицу $$$c$$$ размера $$$n \times m$$$, построенную по следующему правилу: $$$c_{i, j} = a_i \cdot b_j$$$ (то есть $$$a_i$$$, умноженное на $$$b_j$$$). Несложно заметить, что $$$c$$$ также состоит только из нулей и единиц.
Сколько подпрямоугольников размера $$$k$$$, состоящих только из единиц, есть в $$$c$$$?
Подпрямоугольник — это пересечение непрерывного подотрезка строк и непрерывного подотрезка столбцов матрицы. Рассмотрим четыре числа $$$x_1, x_2, y_1, y_2$$$ ($$$1 \le x_1 \le x_2 \le n$$$, $$$1 \le y_1 \le y_2 \le m$$$), тогда подпрямоугольник $$$c[x_1 \dots x_2][y_1 \dots y_2]$$$ — это пересечение строк $$$x_1, x_1+1, x_1+2, \dots, x_2$$$ и столбцов $$$y_1, y_1+1, y_1+2, \dots, y_2$$$.
Размер (площадь) подпрямоугольника — это количество элементов матрицы в нём.
В первой строке содержатся три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$1 \leq n, m \leq 40\,000, 1 \leq k \leq n \cdot m$$$) — длина массива $$$a$$$, длина массива $$$b$$$ и требуемый размер подпрямоугольников.
Во второй строке содержатся $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$0 \leq a_i \leq 1$$$) — элементы массива $$$a$$$.
В третьей строке содержатся $$$m$$$ целых чисел $$$b_1, b_2, \ldots, b_m$$$ ($$$0 \leq b_i \leq 1$$$) — элементы массива $$$b$$$.
Выведите одно целое число — количество подпрямоугольников в $$$c$$$ размера $$$k$$$, состоящих только из единиц.
3 3 2 1 0 1 1 1 1
4
3 5 4 1 1 1 1 1 1 1 1
14
В первом примере матрица $$$c$$$ такова:
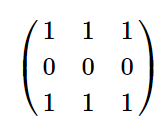
В ней есть $$$4$$$ подпрямоугольника размера $$$2$$$, состоящих только из единиц:
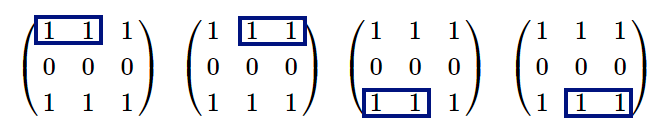
Во втором примере матрица $$$c$$$ такова:
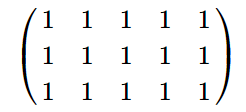
| Название |
|---|




