| Codeforces Round 622 (Div. 2) |
|---|
| Закончено |
Николай только недавно начал заниматься олимпиадным программированием, но уже смог пройти в финал престижной олимпиады. Всего в финале будет $$$n$$$ участников, один из которых Николай. Как и любая хорошая олимпиада, она состоит из двух туров. Уставшие от традиционных правил, в которых участник, решивший наибольшее число задач, побеждает, организаторы придумали альтернативные правила.
Пусть по результатам первого тура участник А занял место $$$x$$$, а по результатам второго — $$$y$$$. Тогда суммарным баллом участника А считается сумма $$$x + y$$$. Итоговое место А определяется как количество участников (включая А), у которых суммарный балл не превосходит суммарный балл А. Обратите внимание, что таким образом некоторые участники могут делить места между собой. Также важно заметить, что и в первом, и во втором туре никакие два участника не поделили место, таким образом для каждого $$$i$$$ от $$$1$$$ до $$$n$$$ ровно один участник занял $$$i$$$-е место в первом и ровно один участник занял $$$i$$$-е место во втором туре.
По окончании олимпиады Николаю сообщили, что он занял $$$x$$$-е место в первом туре, $$$y$$$-е место во втором. Результаты других участников ему неизвестны. В ожидании результатов олимпиады Николай заинтересовался, какое минимальное и максимальное место он может занять, если рассмотреть самый благоприятный для него результат других участников и самый неблагоприятный. Помогите Николаю найти ответ на этот вопрос.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество тестовых случаев, которое надо решить.
Каждая из следующих $$$t$$$ строк содержит целые числа $$$n$$$, $$$x$$$, $$$y$$$ ($$$1 \leq n \leq 10^9$$$, $$$1 \le x, y \le n$$$) — число участников олимпиады, место занятое Николаем в первом туре, место занятое Николаев во втором туре.
Для каждого тестового случая выведите два целых числа — минимальное и максимальное итоговое место, которое может занять Николай.
1
5 1 3
1 3
1
6 3 4
2 6
Пояснение к первому тесту:
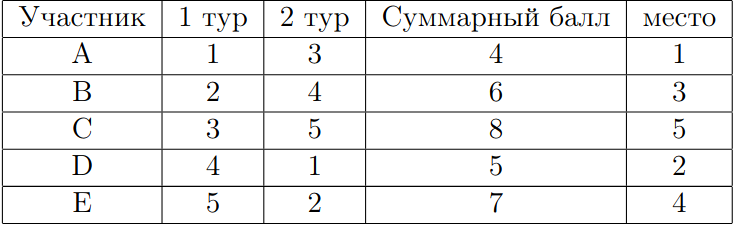
Пусть было 5 участников A-E. Николая обозначим за А. Тогда наиболее благоприятные для Николая результаты олимпиады могли выглядеть так:
Однако результаты олимпиады могли выглядеть и так:
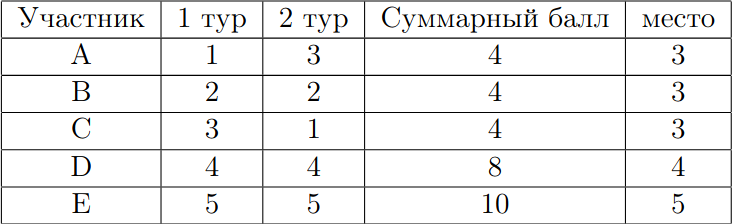
В первом случае Николай занял бы первое место, во втором — третье.
| Название |
|---|




