Это интерактивная задача.
После АС после 13 вердиктов Превышено Время Исполнения по задаче с геометрии, Курони отправился в итальянский ресторан, чтобы отпраздновать это святое достижение. К сожалению, лишний соус дезориентировал его, и он теперь потерялся!
Соединенные Штаты Америки могут быть смоделированы как дерево (хотя стойте...) с $$$n$$$ вершинами. Корень дерева находится в вершине $$$r$$$, в которой находится гостиница Курони.
У Курони есть приложение для телефона, предназначенное для оказания ему помощи в таких экстренных случаях. Чтобы использовать приложение, ему нужно ввести две вершины $$$u$$$ и $$$v$$$, и оно вернет вершину $$$w$$$, которая является наименьшим общим предком этих двух вершин.
Однако, поскольку батарея телефона была почти полностью разряжена во время праздничной вечеринки Курони, он может использовать приложение не более $$$\lfloor \frac{n}{2} \rfloor$$$ раз. После этого телефон разрядится и не останется ничего, чтобы помочь нашему дорогому другу! :(
Поскольку ночь холодная и темная, Курони должен вернуться, чтобы он мог воссоединиться со своей удобной кроватью и подушками. Можете ли вы помочь ему выяснить местоположение своего отеля?
Взаимодействие начинается с чтения одного целого числа $$$n$$$ ($$$2 \le n \le 1000$$$), количества вершин дерева.
Затем прочтите $$$n-1$$$ строку, $$$i$$$-я из которых содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$, $$$x_i \ne y_i$$$), обозначающие, что есть ребро, соединяющее вершины $$$x_i$$$ и $$$y_i$$$. Гарантируется, что ребра сформируют дерево.
После этого, вы можете делать запросы типа "? u v" ($$$1 \le u, v \le n$$$), чтобы найти наименьшего общего предка вершин $$$u$$$ и $$$v$$$.
После запроса считайте результат $$$w$$$ как целое число.
В случае, если ваш запрос не соответствует требованиям, или вы задали более $$$\lfloor \frac{n}{2} \rfloor$$$ запросов, программа выведет $$$-1$$$ и прекратит взаимодействие. Вы получите вердикт Неправильный ответ. Вам нужно завершить работу вашей программы, чтобы не получить другие вердикты.
Когда вы узнаете вершину $$$r$$$, выведите "! $$$r$$$" и выйдите после этого. Этот запрос не учитывается в пределе $$$\lfloor \frac{n}{2} \rfloor$$$.
Обратите внимание, что дерево фиксировано заранее и не будет изменяться во время запросов, то есть интерактор не адаптивен. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат взломов
Для взломов используйте следующий формат:
Первая строка должна содержать два целых числа $$$n$$$ и $$$r$$$ ($$$2 \le n \le 1000$$$, $$$1 \le r \le n$$$), обозначающих количество вершин и вершину с отелем Курони.
$$$i$$$-я из следующих $$$n-1$$$ строк должна содержать два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$) — обозначающих, что есть ребро, соединяющее вершины $$$x_i$$$ и $$$y_i$$$.
Представленные ребра должны сформировать дерево.
6 1 4 4 2 5 3 6 3 2 3 3 4 4
? 5 6 ? 3 1 ? 1 2 ! 4
Обратите внимание, что пример взаимодействия содержит дополнительные пустые строки, чтобы его было легче читать. Реальное взаимодействие не содержит пустых строк, и вы не должны также печатать лишние пустые строки.
Рисунок ниже изображает дерево с примера:
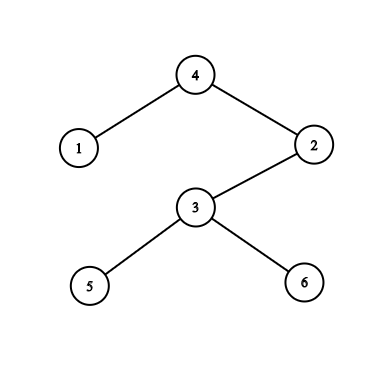
| Название |
|---|




