| Codeforces Round 620 (Div. 2) |
|---|
| Закончено |
Устав от участия в раундах на Codeforces, Гильдонг решил отдохнуть в парке. Он присел на лавку, и заметил двух кроликов, прыгающих поблизости.
Он заметил, что два кролика прыгали навстречу друг другу. Позиции двух кроликов можно задать целочисленными координатами на горизонтальной прямой. Более высокий кролик изначально находится в точке с координатой $$$x$$$, а более низкий — в точке с координатой $$$y$$$ ($$$x \lt y$$$). Каждую секунду, каждый кролик прыгает на другую позицию. Более высокий кролик прыгает в положительном направлении на $$$a$$$, а более низкий прыгает в отрицательном направлении на $$$b$$$.
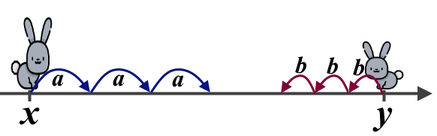
Например, если $$$x=0$$$, $$$y=10$$$, $$$a=2$$$, и $$$b=3$$$. После $$$1$$$-й секунды, кролики будут в точках $$$2$$$ и $$$7$$$. После $$$2$$$-й секунды, оба кролика будет в точке $$$4$$$.
Гильдонг задумался: Будут ли когда-то два кролика в одной точке в один момент времени? Если будут, то через какое время это произойдет? Помогите ему найти такую секунду, после которой оба кролика будут в одной точке.
Каждый тест состоит из одного или более наборов входных данных. В первой строке записано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 1000$$$).
Каждый набор входных данных состоит из ровно одной строки. Строка состоит из четырех целых чисел $$$x$$$, $$$y$$$, $$$a$$$, $$$b$$$ ($$$0 \le x \lt y \le 10^9$$$, $$$1 \le a,b \le 10^9$$$) — текущая позиция более высокого кролика, текущая позиция более низкого кролика, расстояние прыжка более высокого прыжка, расстояние прыжка более низкого кролика, соответственно.
Для каждого набора входных данных, выведите одно целое число — количество секунд, через которое два кролика окажутся в одной точке.
Если два кролика никогда не окажутся в одной точке одновременно, выведите $$$-1$$$.
5 0 10 2 3 0 10 3 3 900000000 1000000000 1 9999999 1 2 1 1 1 3 1 1
2 -1 10 -1 1
Первый набор входных данных примера разобран в условии.
Во втором наборе входных данных примера кролики будут в точках $$$3$$$ и $$$7$$$ на секунде $$$1$$$. На секунде $$$2$$$, они будут в точках $$$6$$$ и $$$4$$$, и можно заметить, что они никогда не будут в одной точке, потому что расстояние между ними будет только увеличиваться.
| Название |
|---|




