| Codeforces Round 619 (Div. 2) |
|---|
| Закончено |
Башар готовится к национальному констесту по программированию. Из-за слишком частого сидения перед компьютером без совершения каких-либо физических действий Башар стал толстеть. Он собирается уйти из программирования после национального контеста и стать актером (как его отец), поэтому ему нужно сбросить вес.
Поэтому, Башар решил пробежать $$$k$$$ километров. Башар собирается бежать в месте, которое выглядит как таблица с $$$n$$$ строками и $$$m$$$ столбцами. В этой таблице есть по две односторонние дороги длинной в один километр между каждой парой соседних по стороне клеток: одна дорога идет от первой клетки ко второй, другая от второй к первой. Поэтому, всего ровно $$$(4 n m - 2n - 2m)$$$ дорог.
Давайте рассмотрим, например $$$n = 3$$$ и $$$m = 4$$$. В этом случае, есть ровно $$$34$$$ дороги. Это картинка, демонстрирующая этот случай (стрелки обозначают дороги):
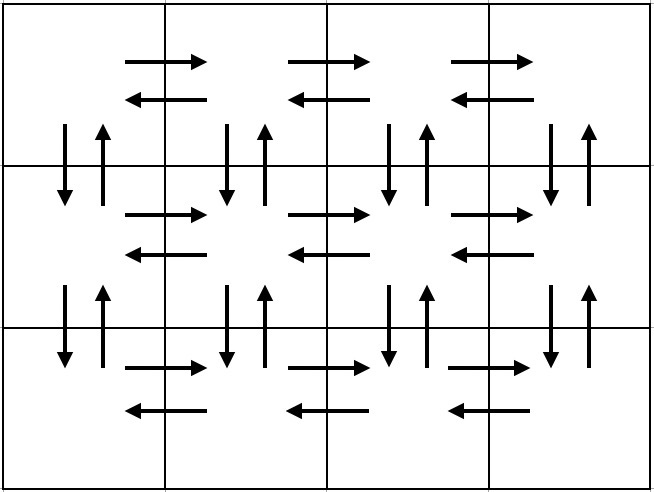
Башар хочет бежать по следующим правилам:
- Он начинает в левой верхней клетке таблицы;
- За один ход он может переместиться на одну клетку вверх (символ 'U'), вниз (символ 'D'), влево (символ 'L') или вправо (символ 'R'). Более формально, если он сейчас находится в клетке в строке $$$i$$$ и в столбце $$$j$$$, то есть в клетке $$$(i, j)$$$, то он переместится:
- в случае 'U' в клетку $$$(i-1, j)$$$;
- в случае 'D' в клетку $$$(i+1, j)$$$;
- в случае 'L' в клетку $$$(i, j-1)$$$;
- в случае 'R' в клетку $$$(i, j+1)$$$;
- Он хочет пробежать ровно $$$k$$$ километров, то есть он хочет совершить ровно $$$k$$$ ходов;
- Башар может закончить в любой клетке таблицы;
- Он не может выходить за пределы таблицы, то есть в любой момент времени он должен находиться в одной из клеток таблицы;
- Башар не хочет, чтобы ему было скучно во время бега, поэтому он не должен посещать одну и ту же дорогу более одного раза. Но он может посещать одну и ту же клетку любое количество раз.
Башар спрашивает вас, можно ли пробежать по таким правилам. Если это возможно, вы должны сказать ему, как он должен бежать.
Вы должны дать ему $$$a$$$ шагов и поскольку Башар не может запомнить слишком много шагов, $$$a$$$ не должно превосходить $$$3000$$$. Для каждого шага вы должны дать ему положительное целое число $$$f$$$ и строчку ходов $$$s$$$ длиной не больше $$$4$$$. Этот шаг означает, что вы должны повторять ходы строки $$$s$$$ $$$f$$$ раз. Он будет выполнять шаги в порядке, в котором вы их вывели.
Например, если шаги это $$$2$$$ RUD, $$$3$$$ UUL, то его ходы будут RUD $$$+$$$ RUD $$$+$$$ UUL $$$+$$$ UUL $$$+$$$ UUL $$$=$$$ RUDRUDUULUULUUL.
Можете ли вы помочь ему и дать ему корректную последовательность шагов, такую что общее расстояние, которое он пробежит равно $$$k$$$ или сказать, что это невозможно?
В единственной строке находится три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$1 \leq n, m \leq 500$$$, $$$1 \leq k \leq 10 ^{9}$$$), которые равны количеству строк, количеству столбцов в таблице и расстоянию, которое Башар хочет пробежать.
Если не существует способа пробежать $$$k$$$ километров, выведите «NO» (без кавычек), иначе выведите «YES» (без кавычек) в первой строке.
Если ответ «YES», во второй строке выведите целое число $$$a$$$ ($$$1 \leq a \leq 3000$$$) — количество шагов, затем выведите $$$a$$$ строк, описывающих шаги.
Для того, чтобы описать шаг, выведите положительное целое число $$$f$$$ ($$$1 \leq f \leq 10^{9}$$$) и строку ходов $$$s$$$ длины не более $$$4$$$. Каждый символ строки $$$s$$$ должен быть равен 'U', 'D', 'L' или 'R'.
Башар будет начинать в левой верхней клетке. Обратите внимание, что он должен пробежать ровно $$$k$$$ километров и не пробежать по одной и той же дороге дважды. Он не должен выходить за пределы таблицы. Он может закончить в любой клетке.
Можно показать, что если можно пробежать ровно $$$k$$$ километров, соблюдая все условия, то можно описать какой-то путь в данных ограничениях на выходные данные.
3 3 4
YES 2 2 R 2 L
3 3 1000000000
NO
3 3 8
YES 3 2 R 2 D 1 LLRR
4 4 9
YES 1 3 RLD
3 4 16
YES 8 3 R 3 L 1 D 3 R 1 D 1 U 3 L 1 D
Ходы, которые Башар собирается сделать в первом тесте это: «RRLL».
Невозможно пробежать $$$1000000000$$$ километров во втором тесте, потому что суммарная длина дорог будет намного меньше, а Башар не может посещать одну и ту же дорогу дважды.
Ходы, которые Башар собирается сделать в третьем тесте это: «RRDDLLRR».
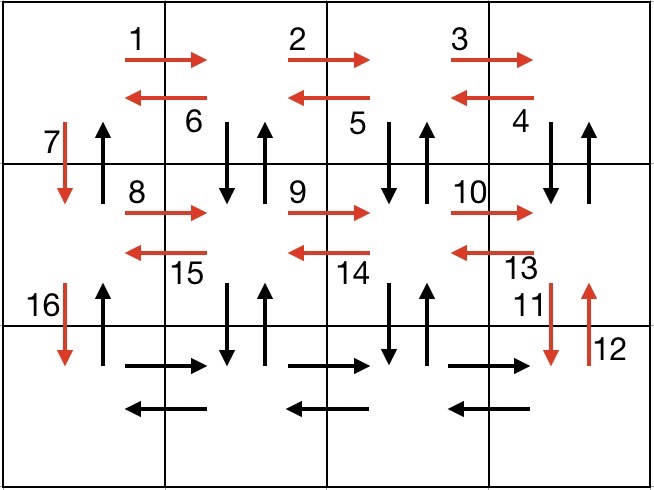
Ходы, которые Башар собирается сделать в пятом тесте это: «RRRLLLDRRRDULLLD». Это картинка его маршрута (дороги вдоль его маршрута покрашены в красный и пронумерованы в порядке, в котором он будет пробегать их):
| Название |
|---|




