D. Вокруг света
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
512 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Ги-Мануэль и Тома планируют $$$144$$$ кругосветных путешествия.

Вам дан простой взвешенный неориентированный связный граф из $$$n$$$ вершин и $$$m$$$ рёбер со следующим ограничением: не существует простого цикла (т. е. цикла, проходящего через каждую вершину не больше раза) длины больше $$$3$$$, проходящего через вершину $$$1$$$. Стоимостью пути (необязательно простого) в этом графе является XOR весов всех рёбер, входящих в этот путь, причём каждое ребро считается столько, сколько раз через него проходит путь.

Однако, путешествия стоимостью $$$0$$$ их не устраивают.

Вы можете выбрать любое подмножество рёбер, инцидентных вершине $$$1$$$, и удалить их. Сколько существует таких множеств, что при их удалении в полученном графе нет нетривиального цикла (необязательно простого) стоимостью $$$0$$$, проходящего через вершину $$$1$$$? Цикл называется нетривиальным, если существует ребро, через которое он проходит нечётное количество раз. Так как ответ может быть большим, выведите его по модулю $$$10^9+7$$$.

Входные данные

Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n,m \le 10^5$$$) — количество вершин и рёбер в графе. $$$i$$$-я из следующих $$$m$$$ строк содержит три целых числа $$$a_i$$$, $$$b_i$$$ и $$$w_i$$$ ($$$1 \le a_i, b_i \le n, a_i \neq b_i, 0 \le w_i < 32$$$) — концы $$$i$$$-го ребра и его вес. Гарантируется, что в графе нет мультирёбер, граф является связным, и не существует простого цикла длины больше $$$3$$$, проходящего через вершину $$$1$$$.

Выходные данные

В единственной строке выведите ответ по модулю $$$10^9+7$$$.

Примеры
Входные данные
6 8
1 2 0
2 3 1
2 4 3
2 6 2
3 4 8
3 5 4
5 4 5
5 6 6
Выходные данные
2
Входные данные
7 9
1 2 0
1 3 1
2 3 9
2 4 3
2 5 4
4 5 7
3 6 6
3 7 7
6 7 8
Выходные данные
1
Входные данные
4 4
1 2 27
1 3 1
1 4 1
3 4 0
Выходные данные
6
Примечание

На рисунках представлены графы из примеров. 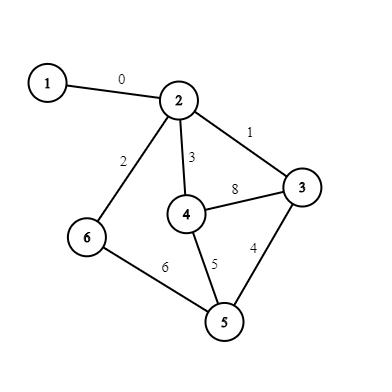В первом примере в графе нет нетривиальных циклов со стоимостью $$$0$$$, так что мы можем как удалить единственное ребро, инцидентное вершине $$$1$$$, так и не удалять. 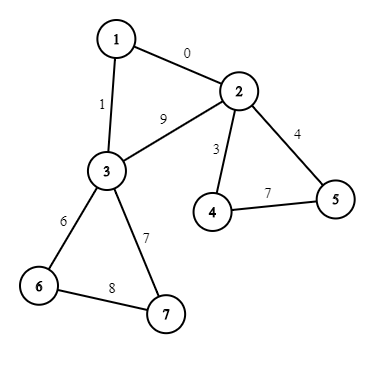Во втором примере если мы не удаляем ребро $$$1-2$$$, то в графе будет цикл $$$1-2-4-5-2-1$$$ со стоимостью $$$0$$$; аналогично, если мы не удаляем ребро $$$1-3$$$, то в графе будет цикл $$$1-3-2-4-5-2-3-1$$$ со стоимостью $$$0$$$. Единственный вариант — удалить оба ребра. 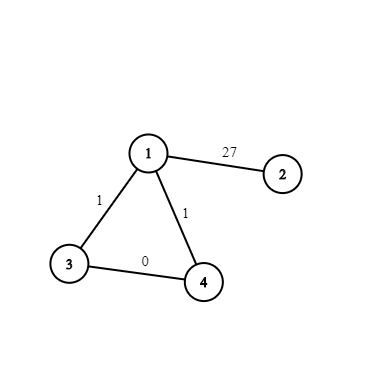В третьем примере подходят все подмножества, кроме тех двух, при которых остаются оба ребра $$$1-3$$$ и $$$1-4$$$.