| Codeforces Round 615 (Div. 3) |
|---|
| Закончено |
Вам задана прямоугольная матрица размера $$$n \times m$$$, состоящая из целых чисел от $$$1$$$ до $$$2 \cdot 10^5$$$. За один ход вы можете:
- выбрать любой элемент матрицы и изменить его значение на любое целое число от $$$1$$$ до $$$n \cdot m$$$, включительно;
- взять любой столбец и сдвинуть его на одну клетку вверх циклически (смотрите пример такого циклического сдвига ниже).
Циклический сдвиг — это операция, в которой выбирается некоторое $$$j$$$ ($$$1 \le j \le m$$$) и присваивается $$$a_{1, j} := a_{2, j}, a_{2, j} := a_{3, j}, \dots, a_{n, j} := a_{1, j}$$$ одновременно.
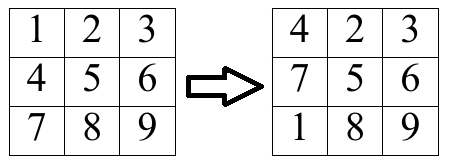 Пример циклического сдвига первого столбца
Пример циклического сдвига первого столбца Вы хотите определить минимальное количество шагов, за которое можно привести матрицу к подобному виду:
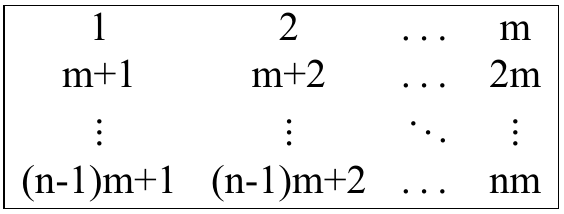
Другими словами, ваша цель — получить матрицу, в которой $$$a_{1, 1} = 1, a_{1, 2} = 2, \dots, a_{1, m} = m, a_{2, 1} = m + 1, a_{2, 2} = m + 2, \dots, a_{n, m} = n \cdot m$$$ (i.e. $$$a_{i, j} = (i - 1) \cdot m + j$$$) за минимальное число шагов.
Первая строка входных данных содержит два целых числа $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 2 \cdot 10^5, n \cdot m \le 2 \cdot 10^5$$$) — размер матрицы.
Следующие $$$n$$$ строк содержат по $$$m$$$ целых чисел в каждой. Число в строке $$$i$$$ на позиции $$$j$$$ равно $$$a_{i, j}$$$ ($$$1 \le a_{i, j} \le 2 \cdot 10^5$$$).
Выведите одно целое число — минимальное число шагов, необходимое, чтобы получить матрицу, в которой $$$a_{1, 1} = 1, a_{1, 2} = 2, \dots, a_{1, m} = m, a_{2, 1} = m + 1, a_{2, 2} = m + 2, \dots, a_{n, m} = n \cdot m$$$ ($$$a_{i, j} = (i - 1)m + j$$$).
3 3 3 2 1 1 2 3 4 5 6
6
4 3 1 2 3 4 5 6 7 8 9 10 11 12
0
3 4 1 6 3 4 5 10 7 8 9 2 11 12
2
В первом тестовом примере можно присвоить $$$a_{1, 1} := 7, a_{1, 2} := 8$$$ и $$$a_{1, 3} := 9$$$, а затем циклически сдвинуть первый, втрой и третий столбцы, таким образом, ответ равен $$$6$$$. Можно показать, что лучшего результата достигнуть невозможно.
Во втором тестовом примере матрица уже является хорошей, поэтому ответ равен $$$0$$$.
В третьем тестовом примере достаточно дважды циклически сдвинуть второй столбец, чтобы получить хорошую матрицу, поэтому ответ равен $$$2$$$.
| Название |
|---|




