| Codeforces Round 616 (Div. 1) |
|---|
| Закончено |
Назовем две строки $$$s$$$ и $$$t$$$ анаграммами друг друга, если можно так переставить символы в строке $$$s$$$, чтобы получить строку, равную $$$t$$$.
Рассмотрим две строки $$$s$$$ и $$$t$$$, являющиеся анаграммами друг друга. Будем говорить, что $$$t$$$ это приводимая анаграмма строки $$$s$$$, если существует такое целое число $$$k \ge 2$$$ и $$$2k$$$ непустых строк $$$s_1, t_1, s_2, t_2, \dots, s_k, t_k$$$, которые удовлетворяют следующим условиям:
- Если мы запишем в линию строки $$$s_1, s_2, \dots, s_k$$$ в таком порядке, то получившаяся строка будет равна $$$s$$$;
- Если мы запишем в линию строки $$$t_1, t_2, \dots, t_k$$$ в таком порядке, то получившаяся строка будет равна $$$t$$$;
- Для всех целых $$$i$$$ между $$$1$$$ и $$$k$$$ включительно, $$$s_i$$$ и $$$t_i$$$ являются анаграммами.
Если таких строк не существует, тогда $$$t$$$ называется неприводимой анаграммой строки $$$s$$$. Обратите внимание, что этот термин определяется только в случае, когда $$$s$$$ и $$$t$$$ это анаграммы.
Например, рассмотрим строку $$$s = $$$ «gamegame». Тогда строка $$$t = $$$ «megamage» это приводимая анаграмма для $$$s$$$, потому что мы можем выбрать, например, $$$s_1 = $$$ «game», $$$s_2 = $$$ «gam», $$$s_3 = $$$ «e» и $$$t_1 = $$$ «mega», $$$t_2 = $$$ «mag», $$$t_3 = $$$ «e»:
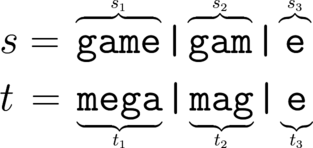
С другой стороны, можно показать, что $$$t = $$$ «memegaga» это неприводимая анаграмма для $$$s$$$.
Вам будет дана строка $$$s$$$ и $$$q$$$ запросов, каждый представляется двумя целыми числами $$$1 \le l \le r \le |s|$$$ (где за $$$|s|$$$ обозначается длина строки $$$s$$$). Для каждого запроса, вы должны определить, имеет ли подстрока строки $$$s$$$, с $$$l$$$-о по $$$r$$$-й символ, включительно, хотя бы одну неприводимую анаграмму.
В первой строке находится строка $$$s$$$, состоящая из строчных символов латинского алфавита ($$$1 \le |s| \le 2 \cdot 10^5$$$).
Во второй строке содержится единственное целое число $$$q$$$ ($$$1 \le q \le 10^5$$$) — количество запросов.
Следующие $$$q$$$ строк содержат по два целых числа $$$l$$$ и $$$r$$$ ($$$1 \le l \le r \le |s|$$$), обозначающие очередной запрос для подстроки $$$s$$$, состоящей из символов с $$$l$$$-о по $$$r$$$-й.
Для каждого запроса, выведите единственную строку, содержащую «Yes» (без кавычек), если соответствующая запросу подстрока имеет хотя бы одну неприводимую анаграмму и «No» (без кавычек), иначе.
aaaaa 3 1 1 2 4 5 5
Yes No Yes
aabbbbbbc 6 1 2 2 4 2 2 1 9 5 7 3 5
No Yes Yes Yes No No
В первом тесте, в первом и третьем запросах, подстрока будет «a» и она имеет саму себя как неприводимую анаграмму, так как две и больше непустые строки, записанные вместе, не смогут дать строку «a». С другой стороны, во втором запросе, подстрока будет «aaa», которая не имеет неприводимых анаграмм: ее единственная анаграмма это она сама и мы можем выбрать $$$s_1 = $$$ «a», $$$s_2 = $$$ «aa», $$$t_1 = $$$ «a», $$$t_2 = $$$ «aa», чтобы показать, что это приводимая анаграмма.
Во втором запросе второго тестового случая, подстрока будет «abb» и она имеет, например, неприводимую анаграмму «bba».
| Название |
|---|




