| Codeforces Round 612 (Div. 1) |
|---|
| Закончено |
В Чилляндии построили бесконечно длинный Линейный Чилляндский Коллайдер (ЛЧК). К ЛЧК подсоединены $$$n$$$ труб c координатами $$$x_i$$$. В момент времени 0 из каждой трубки ЛЧК вылетает протон направо с вероятностью $$$p_i$$$ и с вероятностью $$$(1 - p_i)$$$ — влево. Протон $$$i$$$ разогнан до скорости $$$v_i$$$. Длительность эксперимента определяется как время до первого столкновения двух протонов. В случае, если столкновений не произойдет, длительность эксперимента полагается равной нулю.
Найдите математическое ожидание длительности эксперимента.
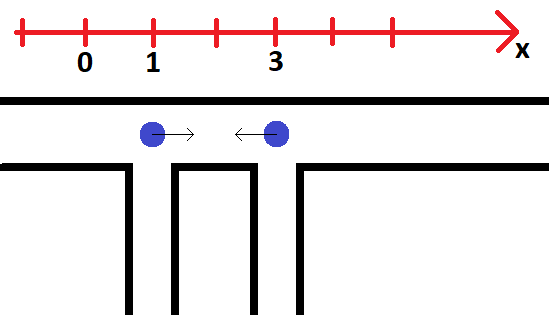Иллюстрация к первому примеруПервая строка входных данных содержит одно целое число $$$n$$$ — количество труб ($$$1 \le n \le 10^5$$$). В следующих $$$n$$$ строках содержится по три целых числа $$$x_i$$$, $$$v_i$$$, $$$p_i$$$ — координата $$$i$$$-й трубы, скорость $$$i$$$-го протона, и вероятность вылета $$$i$$$-го протона вправо в процентах ($$$-10^9 \le x_i \le 10^9, 1 \le v \le 10^6, 0 \le p_i \le 100$$$). Гарантируется, что все $$$x_i$$$ различны и отсортированы в порядке возрастания.
Можно показать, что ответ всегда можно представить в виде дроби $$$P/Q$$$, где $$$P$$$ — целое число, а $$$Q$$$ — натуральное число, не кратное $$$998\,244\,353$$$. В таком случае выведите $$$P \cdot Q^{-1}$$$ по модулю $$$998\,244\,353$$$.
2 1 1 100 3 1 0
1
3 7 10 0 9 4 86 14 5 100
0
4 6 4 50 11 25 50 13 16 50 15 8 50
150902884
