| Codeforces Round 612 (Div. 1) |
|---|
| Закончено |
Евлампию подарили корневое дерево, вершины которого пронумерованы от $$$1$$$ до $$$n$$$. В каждой $$$i$$$-й вершине написано число $$$a_i$$$. Евлампий посчитал для каждой вершины $$$i$$$ величину $$$c_i$$$ — количество вершин $$$j$$$ в поддереве вершины $$$i$$$, для которых $$$a_j < a_i$$$.
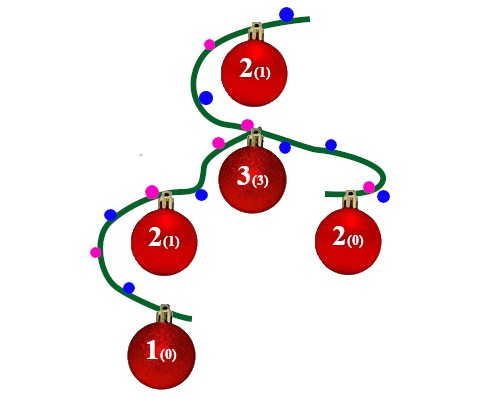Иллюстрация ко второму примеру, первым написано $$$a_i$$$, а в скобках написано $$$c_i$$$После нового года Евлампий не смог вспомнить, каким был его подарок! Он помнит дерево и значения $$$c_i$$$, однако совсем забыл, какие числа $$$a_i$$$ были написаны в вершинах. Помогите ему восстановить исходные числа!
В первой строке содержится целое число $$$n$$$ $$$(1 \leq n \leq 2000)$$$ — количество вершин в дереве.
Далее в $$$n$$$ строках идёт описание вершин дерева: в $$$i$$$-й строке находятся два целых числа $$$p_i$$$ и $$$c_i$$$ ($$$0 \leq p_i \leq n$$$; $$$0 \leq c_i \leq n-1$$$), где $$$p_i$$$ — номер родителя вершины $$$i$$$ или $$$0$$$ для корня дерева, а $$$c_i$$$ — количество вершин $$$j$$$ в поддереве вершины $$$i$$$, для которых $$$a_j < a_i$$$.
Гарантируется, что значения $$$p_i$$$ задают некоторое корневое дерево из $$$n$$$ вершин.
Если решение существует, то в первой строке выведите «YES», а во второй строке выведите $$$n$$$ чисел $$$a_i$$$ $$$(1 \leq a_i \leq {10}^{9})$$$ — искомые числа, которые были записаны в вершинах дерева. Если решений несколько, выведите любое из них. Можно показать, что если решение существует, то также существует решение, где все $$$a_i$$$ лежат от $$$1$$$ до $$$10^9$$$.
Если же решения не существует, то выведите «NO».
3 2 0 0 2 2 0
YES 1 2 1
5 0 1 1 3 2 1 3 0 2 0
YES 2 3 2 1 2
