| Codeforces Round 605 (Div. 3) |
|---|
| Закончено |
Недавно вы купили робота-снегохода и принесли его домой. Ваш дом — это клетка $$$(0, 0)$$$ на бесконечной координатной сетке.
Вы также получили последовательность инструкций этого робота. Она записана в виде строки $$$s$$$, состоящей из символов 'L', 'R', 'U' и 'D'. Если сейчас робот находится в клетке $$$(x, y)$$$, он может передвинуться в одну из смежных клеток (зависит от текущей инструкции).
- Если текущая инструкция — 'L', тогда робот может передвинуться влево в $$$(x - 1, y)$$$;
- если текущая инструкция — 'R', тогда робот может передвинуться вправо в $$$(x + 1, y)$$$;
- если текущая инструкция — 'U', тогда робот может передвинуться вверх в $$$(x, y + 1)$$$;
- если текущая инструкция — 'D', тогда робот может передвинуться вниз в $$$(x, y - 1)$$$.
Вы заметили предупреждение на последней странице руководства: если робот посетит какую-то клетку (кроме $$$(0, 0)$$$) дважды, то он сломается.
Таким образом, последовательность инструкций является корректной, если робот начинает в клетке $$$(0, 0)$$$, выполняет заданные инструкции, не посещает никакую клетку, кроме $$$(0, 0)$$$, два или более раз и заканчивает свой путь в клетке $$$(0, 0)$$$. Также клетка $$$(0, 0)$$$ должна быть посещена не более двух раз: в начале и в конце (если путь пустой, то она будет посещена только единожды). Например, следующие последовательности инструкций являются корректными: «UD», «RL», «UUURULLDDDDLDDRRUU», а следующие являются некорректными: «U» (конечная клетка не равна $$$(0, 0)$$$) и «UUDD» (клетка $$$(0, 1)$$$ посещается дважды).
Но изначальная последовательность инструкций может быть некорректной. Вы не хотите, чтобы ваш робот сломался, поэтому вы решили перепрограммировать его следующим образом: вы удалите какие-то (возможно, все или никакие) инструкции из изначальной последовательности инструкций, затем поменяете порядок оставшихся инструкций так, как хотите, и включите вашего робота, который начнет движение.
Ваша задача — удалить минимальное количество инструкций из изначальной последовательности и поменять порядок оставшихся инструкций таким образом, чтобы последовательность стала корректной. Вам необходимо вывести максимальную по длине корректную последовательность инструкций, которую вы можете получить.
Заметьте, что вам необходимо выбрать любой порядок оставшихся инструкций (нет необходимости минимизировать количество обменов или какую-либо другую похожую метрику).
Вам необходимо ответить на $$$q$$$ независимых наборов входных данных.
Первая строка входных данных содержит одно целое число $$$q$$$ ($$$1 \le q \le 2 \cdot 10^4$$$) — количество наборов входных данных.
Следующие $$$q$$$ строк содержат наборы входных данных. $$$i$$$-й набор входных данных задан строкой $$$s$$$, состоящей из не менее, чем $$$1$$$ и не более, чем $$$10^5$$$ символов 'L', 'R', 'U' и 'D' — изначальной последовательности инструкций.
Гарантируется, что сумма $$$|s|$$$ (где $$$|s|$$$ — длина $$$s$$$) не превосходит $$$10^5$$$ по всем наборам входных данных ($$$\sum |s| \le 10^5$$$).
Выведите ответ на каждый набор входных данных. В первой строке выведите максимальное количество оставшихся инструкций. Во второй строке выведите корректную последовательность оставшихся инструкций $$$t$$$, которую робот сможет выполнить. Ходы выполняются слева направо в порядке выведенной последовательности. Если существует несколько возможных ответов, выведите любой. Если ответ равен $$$0$$$, вам разрешается вывести пустую строку (но вы можете не выводить ее).
6 LRU DURLDRUDRULRDURDDL LRUDDLRUDRUL LLLLRRRR URDUR LLL
2 LR 14 RUURDDDDLLLUUR 12 ULDDDRRRUULL 2 LR 2 UD 0
В первом наборе входных данных существует только два правильных ответа: «LR» и «RL».
Картинка, соответствующая второму набору входных данных:
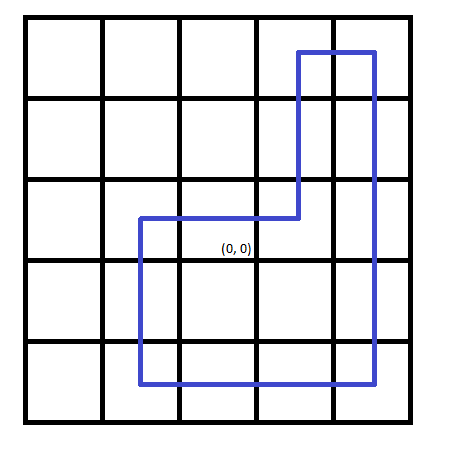 Заметьте, что направление обхода неважно
Заметьте, что направление обхода неважно Другим корректным ответом на третий набор входных данных является «URDDLLLUURDR».
| Название |
|---|




