| Good Bye 2019 |
|---|
| Закончено |
Дано целое число $$$k$$$ и доска $$$2^k \times 2^k$$$, в клетках которой записаны числа, клетка $$$(i, j)$$$ изначально содержит число $$$a_{ij}$$$. Доска считается тором, то есть, клетка справа от $$$(i, 2^k)$$$ это $$$(i, 1)$$$, а клетка вниз от $$$(2^k, i)$$$ это $$$(1, i)$$$. Также дана клетчатая фигурка $$$F$$$, состоящая из $$$t$$$ клеток, где $$$t$$$ нечетное. $$$F$$$ не обязана быть связной.
Мы можем выполнять следующую операцию: положить $$$F$$$ на доску (разрешены только параллельные переносы, повороты и симметрии запрещены). Теперь выберите произвольное неотрицательное число $$$p$$$. После этого, для каждой клетки $$$(i, j)$$$, покрытой $$$F$$$, замените $$$a_{ij}$$$ на $$$a_{ij}\oplus p$$$, где $$$\oplus$$$ обозначает операцию побитового исключающего ИЛИ.
Более формально, пусть $$$F$$$ задана клетками $$$(x_1, y_1), (x_2, y_2), \dots, (x_t, y_t)$$$. Тогда вы можете проделать следующую операцию: выбрать любые $$$x, y$$$ с $$$1\le x, y \le 2^k$$$, любое неотрицательное число $$$p$$$, и для каждого $$$i$$$ от $$$1$$$ до $$$n$$$ заменить число в клетке $$$(((x + x_i - 1)\bmod 2^k) + 1, ((y + y_i - 1)\bmod 2^k) + 1)$$$ на $$$a_{((x + x_i - 1)\bmod 2^k) + 1, ((y + y_i - 1)\bmod 2^k) + 1}\oplus p$$$.
Мы хотим сделать все числа равными $$$0$$$. Можем ли мы этого достичь? Если да, то найдите наименьшее возможное число операций, с помощью которых этого можно добиться.
Первая строка содержит единственное целое число $$$k$$$ ($$$1 \le k \le 9$$$).
$$$i$$$-я из следующих $$$2^k$$$ строк содержит $$$2^k$$$ целых чисел $$$a_{i1}, a_{i2}, \dots, a_{i2^k}$$$ ($$$0 \le a_{ij} < 2^{60}$$$) — изначальные значения чисел в $$$i$$$-й строке доски.
Следующая строка содержит единственное целое число $$$t$$$ ($$$1\le t \le \min(99, 4^k)$$$, $$$t$$$ нечетное) — количество клеток фигуры.
$$$i$$$-я из следующих $$$t$$$ строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le 2^k$$$), описывающих позицию $$$i$$$-й клетки фигуры.
Гарантируется, что все клетки различны, но не гарантируется, что фигура связная.
Если невозможно сделать все числа на доске равными $$$0$$$ с этими операциями, выведите $$$-1$$$.
Иначе, выведите единственное число — минимальное количество операций, необходимых, чтобы это сделать. Можно показать, что если возможно сделать все числа равными $$$0$$$, это можно сделать за не более чем $$$10^{18}$$$ операций.
2 5 5 5 5 2 6 2 3 0 0 2 0 0 0 0 0 5 1 1 1 2 1 3 1 4 2 4
3
Фигурка и операции для примера приведены ниже:
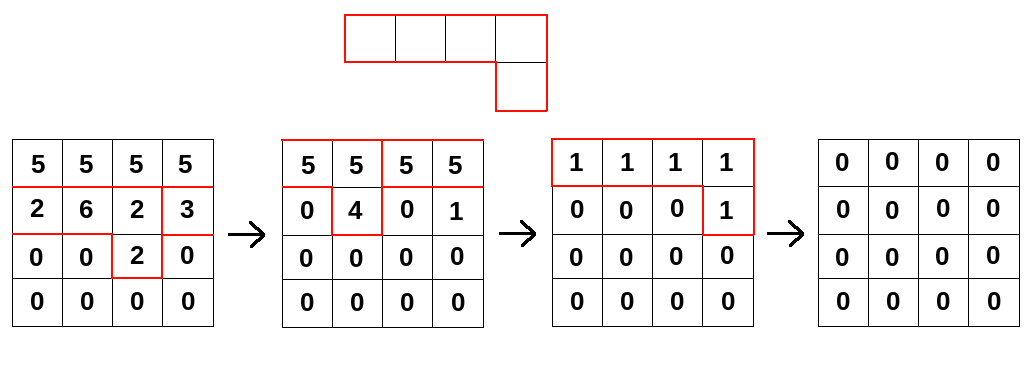
| Название |
|---|




