| Codeforces Round 603 (Div. 2) |
|---|
| Закончено |
Электросеть дворцов в Берляндии состоит из 2-х сетей: основной и запасной. Провода во дворцах сделаны из дорогого материала, поэтому их продажа будет отличной идеей!
Каждая из сетей (основная и запасная) имеет главный узел (он имеет номер $$$1$$$), из которого ток поступает на другие узлы сети. Все узлы доступны от главного по единственному пути. В обеих сетях количество узлов, из которых ток не распространяется дальше, равно $$$n$$$.
Иными словами, каждая из сетей является отдельным корневым ориентированным деревом с $$$n$$$ листьями и с корнем в вершине $$$1$$$. В каждом дереве свои вершины и своя независимая нумерация вершин.
Кроме электросетей во дворце есть $$$n$$$ приборов, каждый из которых соединён с одним из узлов основной и с одним из узлов запасной сети. Приборы соединяются только с такими узлами, из которых ток не распространяется далее (то есть, которые являются листьями). Каждый такой узел (лист дерева) соединён ровно с одним прибором.
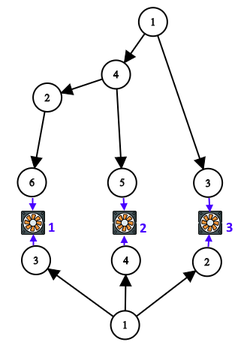 В этом примере основная сеть содержит $$$6$$$ узлов (изображена сверху), а запасная — $$$4$$$ узла (изображена снизу). Количество приборов равно $$$3$$$, они пронумерованы синим цветом.
В этом примере основная сеть содержит $$$6$$$ узлов (изображена сверху), а запасная — $$$4$$$ узла (изображена снизу). Количество приборов равно $$$3$$$, они пронумерованы синим цветом. Гарантируется, что вся электросеть (две сети и $$$n$$$ приборов) может быть изображена на схеме способом, аналогичным картинке выше:
- основная сеть будет составлять дерево сверху, в котором все провода ведут в направлении «сверху вниз»,
- запасная сеть будет составлять дерево снизу, в котором все провода ведут в направлении «снизу вверх»,
- приборы — горизонтальный ряд между ними, пронумерованный от $$$1$$$ до $$$n$$$ слева направо,
- провода между узлами сетей изображены непересекающимися отрезками.
Формально, для каждого дерева существует такой обход в глубину из вершины $$$1$$$, что его листья посещаются в порядке их присоединения к приборам $$$1, 2, \dots, n$$$ (то есть сначала узел, присоединенный к прибору $$$1$$$, затем узел, присоединенный к прибору $$$2$$$, и так далее).
Предприниматель хочет продать (удалить) максимальное количество проводов так, чтобы на каждый прибор поступал ток из хотя бы одной сети. Иначе говоря, для каждого прибора должен существовать путь до главного узла сети (основной или запасной), проходящий по проводам сети от этого главного узла.
В первой строке записано целое число $$$n$$$ ($$$1 \le n \le 1000$$$) — количество приборов во дворце.
В следующей строке записано целое число $$$a$$$ ($$$1 + n \le a \le 1000 + n$$$) — количество узлов в основной электросети.
В следующей строке содержатся $$$a - 1$$$ целых чисел $$$p_i$$$ ($$$1 \le p_i \le a$$$). Каждое число $$$p_i$$$ задает провод от $$$p_i$$$-го узла к $$$(i + 1)$$$-му.
В следующей строке записаны $$$n$$$ чисел $$$x_i$$$ ($$$1 \le x_i \le a$$$) — номер узла в основной электросети, с которым соединен $$$i$$$-й электроприбор.
В следующей строке записано целое число $$$b$$$ ($$$1 + n \le b \le 1000 + n$$$) — количество узлов в запасной электросети.
В следующей строке содержатся $$$b - 1$$$ целых чисел $$$q_i$$$ ($$$1 \le q_i \le b$$$). Каждое число $$$q_i$$$ задает провод от $$$q_i$$$-го узла к $$$(i + 1)$$$-му.
В следующей строке записаны $$$n$$$ чисел $$$y_i$$$ ($$$1 \le y_i \le b$$$) — номер узла в запасной электросети, с которым соединен $$$i$$$-й электроприбор.
Гарантируется, что каждая сеть представляет собой дерево, у каждого из которых ровно $$$n$$$ листьев, причем каждый лист соединен с одним прибором. Также гарантируется, что для каждой сети существует такой порядок обхода в глубину из вершины $$$1$$$, что листы появляются в данном обходе в порядке нумерации соответствующих приборов.
Выведите единственное целое число — максимальное количество проводов, которые можно удалить из сети так, чтобы каждый прибор продолжил получать электрический ток.
3 6 4 1 1 4 2 6 5 3 4 1 1 1 3 4 2
5
4 6 4 4 1 1 1 3 2 6 5 6 6 6 1 1 1 5 4 3 2
6
5 14 1 1 11 2 14 14 13 7 12 2 5 6 1 9 8 3 10 4 16 1 1 9 9 2 5 10 1 14 3 7 11 6 12 2 8 16 13 4 15
17
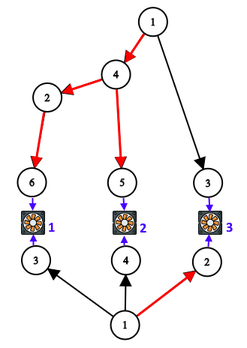
Для первого примера ниже на картинке изображен один из возможных вариантов решения (красным цветом отмечены провода, которые можно удалить):
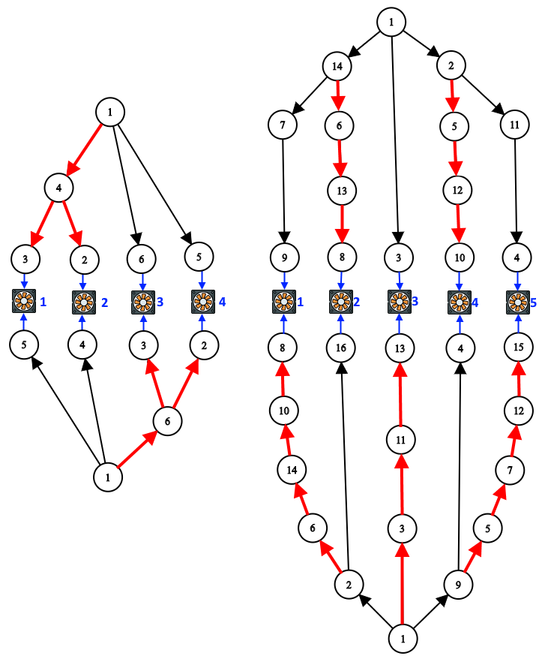
Второй и третий примеры изображены ниже:
| Название |
|---|




