| Codeforces Round 598 (Div. 3) |
|---|
| Закончено |
Вы стоите около реки ширины $$$n$$$. Левым берегом реки является клетка $$$0$$$, а правым берегом является клетка $$$n + 1$$$ (более формально, река может быть представлена как последовательность из $$$n + 2$$$ клеток, пронумерованных от $$$0$$$ до $$$n + 1$$$). Также на реке находятся $$$m$$$ деревянных платформ, $$$i$$$-я платформа имеет длину $$$c_i$$$ (таким образом, $$$i$$$-я платформа занимает $$$c_i$$$ последовательных клеток реки). Гарантируется, что сумма длин платформ не превосходит $$$n$$$.
Вы стоите в клетке $$$0$$$ и хотите каким-то образом достичь клетку $$$n+1$$$. Если вы стоите в позиции $$$x$$$, вы можете прыгнуть в любую позицию в отрезке $$$[x + 1; x + d]$$$. Тем не менее, вы очень не любите воду, поэтому вы можете прыгать только в такие клетки, что они принадлежат каким-то деревянным платформам. Например, если $$$d=1$$$, вы можете прыгать только в следующую позицию (если она принадлежит деревянной платформе). Можете считать, что клетки $$$0$$$ и $$$n+1$$$ принадлежат деревянным платформам.
Вы хотите знать, возможно ли достичь $$$n+1$$$ из $$$0$$$, если вы можете двигать платформы влево и вправо произвольное количество раз (возможно, нулевое) при условии, что они не должны пересекать друг друга (но две платформы могут касаться друг с другом). Это также значит, что вы не можете изменять относительный порядок платформ.
Заметьте, что вы можете двигать платформы до тех пор, пока не начали прыгать (другими словами, вы сначала двигаете платформы, а затем начинаете прыгать).
Например, если $$$n=7$$$, $$$m=3$$$, $$$d=2$$$ и $$$c = [1, 2, 1]$$$, то один из способов достичь $$$8$$$ из $$$0$$$ показан ниже:
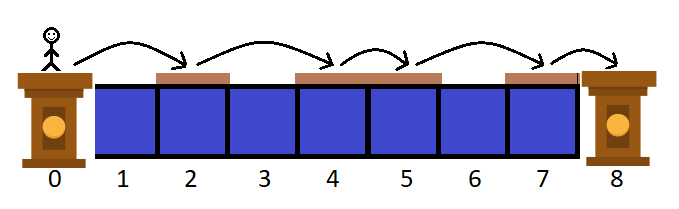Первый пример: $$$n=7$$$. Первая строка входных данных содержит три целых числа $$$n$$$, $$$m$$$ и $$$d$$$ ($$$1 \le n, m, d \le 1000, m \le n$$$) — ширина реки, количество платформ и максимальная дистанция прыжка соответственно.
Вторая строка входных данных содержит $$$m$$$ целых чисел $$$c_1, c_2, \dots, c_m$$$ ($$$1 \le c_i \le n, \sum\limits_{i=1}^{m} c_i \le n$$$), где $$$c_i$$$ равно длине $$$i$$$-й платформы.
Если невозможно достичь $$$n+1$$$ из $$$0$$$, выведите NO в первой строке. Иначе выведите YES в первой строке и массив $$$a$$$ длины $$$n$$$ во второй строке — последовательность клеток реки (исключая клетки $$$0$$$ и $$$n + 1$$$).
Если клетка $$$i$$$ не принадлежит никакой платформе, то $$$a_i$$$ должно быть равно $$$0$$$. Иначе оно должно быть равно индексу платформы (в $$$1$$$-индексации, платформы пронумерованы от $$$1$$$ до $$$m$$$ в порядке входных данных), к которой принадлежит клетка $$$i$$$.
Заметьте, что все $$$a_i$$$, равные $$$1$$$, должны образовывать непрерывный отрезок массива $$$a$$$ длины $$$c_1$$$, все $$$a_i$$$, равные $$$2$$$, должны образовывать непрерывный отрезок массива $$$a$$$ длины $$$c_2$$$, ..., все $$$a_i$$$, равные $$$m$$$, должны образовывать непрерывный отрезок массива $$$a$$$ длины $$$c_m$$$. Самая левая позиция $$$2$$$ в $$$a$$$ должна быть больше, чем самая правая позиция $$$1$$$, самая левая позиция $$$3$$$ в $$$a$$$ должна быть больше, чем самая правая позиция $$$2$$$, ..., самая левая позиция $$$m$$$ в $$$a$$$ должна быть больше, чем самая правая позиция $$$m-1$$$.
Посмотрите примеры выходных данных для лучшего понимания.
7 3 2 1 2 1
YES 0 1 0 2 2 0 3
10 1 11 1
YES 0 0 0 0 0 0 0 0 0 1
10 1 5 2
YES 0 0 0 0 1 1 0 0 0 0
Рассмотрим первый тестовый пример: ответ равен $$$[0, 1, 0, 2, 2, 0, 3]$$$. Последовательность прыжков, которые вы выполняете, равна $$$0 \rightarrow 2 \rightarrow 4 \rightarrow 5 \rightarrow 7 \rightarrow 8$$$.
Рассмотрим второй тестовый пример: неважно, как поставить платформу, так как вы всегда можете допрыгнуть из $$$0$$$ в $$$11$$$.
Рассмотрим третий тестовый пример: ответ равен $$$[0, 0, 0, 0, 1, 1, 0, 0, 0, 0]$$$. Последовательность прыжков, которые вы выполняете, равна $$$0 \rightarrow 5 \rightarrow 6 \rightarrow 11$$$.
