| Codeforces Round 601 (Div. 1) |
|---|
| Закончено |
Это — интерактивная задача.
У Кханя есть $$$n$$$ точек в декартовой системе координат, которые обозначаются как $$$a_1, a_2, \ldots, a_n$$$. Все координаты точек — целые числа от $$$-10^9$$$ до $$$10^9$$$ включительно. Нет трех коллинеарных точек. Он говорит, что эти точки являются вершинами выпуклого многоугольника; другими словами, существует перестановка $$$p_1, p_2, \ldots, p_n$$$ целых чисел от $$$1$$$ до $$$n$$$, такая, что многоугольник $$$a_{p_1} a_{p_2} \ldots a_{p_n}$$$ является выпуклым и вершины перечислены против часовой стрелки.
Кхань дает вам число $$$n$$$, но не координаты своих точек. Ваша задача — угадать вышеуказанную перестановку, задав несколько запросов. В каждом запросе вы даете Кханю $$$4$$$ целых чисел $$$t$$$, $$$i$$$, $$$j$$$, $$$k$$$; где либо $$$t = 1$$$, либо $$$t = 2$$$; и $$$i$$$, $$$j$$$, $$$k$$$ — это три различных индекса от $$$1$$$ до $$$n$$$ включительно. В ответ Хан говорит вам:
- Если $$$t = 1$$$, то площадь треугольника $$$a_ia_ja_k$$$ умноженную на $$$2$$$.
- Если $$$t = 2$$$, то знак векторного произведения двух векторов $$$\overrightarrow{a_ia_j}$$$ и $$$\overrightarrow{a_ia_k}$$$.
Напомним, что векторное произведение вектора $$$\overrightarrow{a} = (x_a, y_a)$$$ и вектора $$$\overrightarrow{b} = (x_b, y_b)$$$ — это целое число $$$x_a \cdot y_b - x_b \cdot y_a$$$. Знак числа равен $$$1$$$, если оно положительное, и $$$-1$$$ иначе. Можно показать, что векторное произведение в запросах никогда не будет $$$0$$$.
Вы можете задать не более $$$3 \cdot n$$$ запросов.
Обратите внимание, что Кхань фиксирует координаты своих точек и не меняет их, отвечая на ваши запросы. Вам не нужно угадывать координаты. В вашей перестановке $$$a_{p_1}a_{p_2}\ldots a_{p_n}$$$, $$$p_1$$$ должен быть равен $$$1$$$ и все индексы вершин должны быть перечисленны против часовой стрелки.
Сначала считайте целое число $$$n$$$ ($$$3 \leq n \leq 1\,000$$$) — количество вершин.
Чтобы задать запрос, выведите $$$4$$$ целых числа $$$t$$$, $$$i$$$, $$$j$$$, $$$k$$$ ($$$1 \leq t \leq 2$$$, $$$1 \leq i, j, k \leq n$$$) на отдельной строке. $$$i$$$, $$$j$$$ и $$$k$$$ должны быть различны.
После этого считайте ответ на запрос. Можно показать, что ответ на любой запрос всегда целое число.
Когда вы найдете перестановку, выведите $$$0$$$. Затем выведите $$$n$$$ целых чисел $$$p_1, p_2, \ldots, p_n$$$ на той же строке.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат взломов
Для взломов используйте следующий формат:
Первая строка должна содержать целое число $$$n$$$ ($$$3 \leq n \leq 1\,000$$$) — количество вершин.
$$$i$$$-я из следующих $$$n$$$ строк должна содержать два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$-10^9 \le x_i, y_i \le 10^9$$$) — координаты точки $$$a_i$$$.
6 15 -1 1
1 1 4 6 2 1 5 6 2 2 1 4 0 1 3 4 2 6 5
Рисунок ниже показывает спрятанный многоугольник в примере:
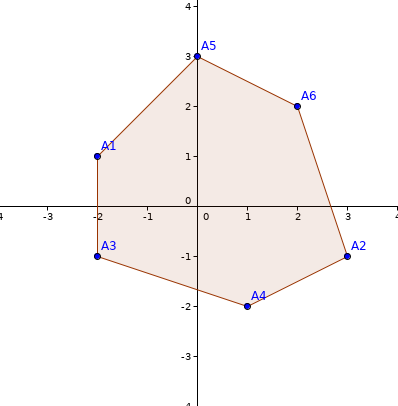
Взаимодействие в примере идет следующим образом:
- Участник считывает $$$n = 6$$$.
- Участник задает запрос $$$t = 1$$$, $$$i = 1$$$, $$$j = 4$$$, $$$k = 6$$$.
- Жюри отвечает $$$15$$$. Площадь $$$A_1A_4A_6$$$ равна $$$7.5$$$. Обратите внимание, что ответ — это площадь умноженная на два.
- Участник задает запрос $$$t = 2$$$, $$$i = 1$$$, $$$j = 5$$$, $$$k = 6$$$.
- Жюри отвечает $$$-1$$$. Векторное произведение $$$\overrightarrow{A_1A_5} = (2, 2)$$$ и $$$\overrightarrow{A_1A_6} = (4, 1)$$$ равно $$$-2$$$. Знак $$$-2$$$ равен $$$-1$$$.
- Участник задает запрос $$$t = 2$$$, $$$i = 2$$$, $$$j = 1$$$, $$$k = 4$$$.
- Жюри отвечает $$$1$$$. Векторное произведение $$$\overrightarrow{A_2A_1} = (-5, 2)$$$ и $$$\overrightarrow{A_2A_4} = (-2, -1)$$$ равно $$$1$$$. Знак $$$1$$$ равен $$$1$$$.
- Участник отвечает $$$(1, 3, 4, 2, 6, 5)$$$.
| Название |
|---|




