| Codeforces Round 600 (Div. 2) |
|---|
| Закончено |
Вам дан простой, неориентированный, связный взвешенный граф с $$$n$$$ вершинами и $$$m$$$ ребрами.
Вершины пронумерованы от $$$1$$$ до $$$n$$$. Есть ровно $$$k$$$ центров (точек перезарядки), находящихся в вершинах $$$1, 2, \ldots, k$$$.
Рассмотрим робота, двигающегося по этому графу, с батареей емкости $$$c$$$, пока не фиксированной конструктором. В любой момент времени батарея может содержать целое количество $$$x$$$ энергии от $$$0$$$ до $$$c$$$ включительно.
Переход по ребру веса $$$w_i$$$ возможен, только если $$$x \ge w_i$$$, и это стоит $$$w_i$$$ энергии ($$$x := x - w_i$$$).
Когда робот достигает центра, его батарея полностью перезаряжается ($$$x := c$$$).
Вам дано $$$q$$$ независимых миссий, в $$$i$$$-й миссии роботу требуется добраться от центра $$$a_i$$$ до центра $$$b_i$$$.
Для каждой миссии, вам требуется найти минимальную емкость батареи, которая требуется, чтобы пройти эту миссию.
В первой строке записано четыре целых числа $$$n$$$, $$$m$$$, $$$k$$$ и $$$q$$$ ($$$2 \le k \le n \le 10^5$$$ и $$$1 \le m, q \le 3 \cdot 10^5$$$).
В $$$i$$$-й из следующих $$$m$$$ строк записаны три целых числа $$$u_i$$$, $$$v_i$$$ и $$$w_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$, $$$1 \le w_i \le 10^9$$$), означающих, что в графе есть ребро между вершинами $$$u$$$ и $$$v$$$, с весом $$$w_i$$$.
Гарантируется, что данный граф простой (в нем нет петель, между каждой парой вершин есть не более одного ребра) и связный.
В $$$i$$$-й из следующих $$$q$$$ строк записаны два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \le a_i, b_i \le k$$$, $$$a_i \neq b_i$$$).
Вам нужно вывести $$$q$$$ строк, $$$i$$$-я из них должна содержать одно целое число: минимальная емкость, которая нужна, чтобы пройти $$$i$$$-ю миссию.
10 9 3 1 10 9 11 9 2 37 2 4 4 4 1 8 1 5 2 5 7 3 7 3 2 3 8 4 8 6 13 2 3
12
9 11 3 2 1 3 99 1 4 5 4 5 3 5 6 3 6 4 11 6 7 21 7 2 6 7 8 4 8 9 3 9 2 57 9 3 2 3 1 2 3
38 15
В первом примере, граф является цепочкой $$$10 - 9 - 2^C - 4 - 1^C - 5 - 7 - 3^C - 8 - 6$$$, где центрами являются вершины $$$1$$$, $$$2$$$ and $$$3$$$.
Для миссии $$$(2, 3)$$$, существует только один простой путь. Вот пример прохождения этой миссии с емкостью $$$12$$$.
- Робот начинает в вершине $$$2$$$, с $$$c = 12$$$ энергии.
- Робот использует ребро веса $$$4$$$.
- Робот дошел до вершины $$$4$$$, с $$$12 - 4 = 8$$$ энергии.
- Робот использует ребро веса $$$8$$$.
- Робот дошел до вершины $$$1$$$ с $$$8 - 8 = 0$$$ энергии.
- Робот на центре, поэтому его батарея перезаряжается. Теперь у него есть $$$c = 12$$$ энергии.
- Робот использует ребро веса $$$2$$$.
- Робот находится в вершине $$$5$$$, с $$$12 - 2 = 10$$$ очками энергии.
- Робот использует ребро веса $$$3$$$.
- Робот находится в вершине $$$7$$$, с $$$10 - 3 = 7$$$ очками энергии.
- Робот использует ребро веса $$$2$$$.
- Робот находится в вершине $$$3$$$, с $$$7 - 2 = 5$$$ очками энергии.
- Робот на центре, поэтому его батарея перезаряжается. Теперь у него есть $$$c = 12$$$ энергии.
- Конец симуляции
Обратите внимание, что если бы $$$c$$$ было меньше $$$12$$$, у нас было бы меньше $$$8$$$ энергии в вершине $$$4$$$, поэтому было бы невозможно воспользоваться ребром $$$4 \leftrightarrow 1$$$ веса $$$8$$$. Таким образом $$$12$$$ это минимальная возможная емкость, которой хватит, для прохождения миссии.
—
Граф во втором примере описан здесь (центры это красные вершины):
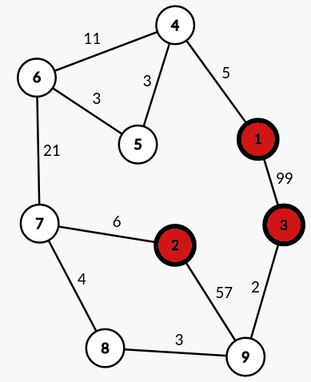
Робот может выполнить миссию $$$(3, 1)$$$ с батареей емкости $$$c = 38$$$, испольуя путь $$$3 \rightarrow 9 \rightarrow 8 \rightarrow 7 \rightarrow 2 \rightarrow 7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 1$$$
Робот может выполнить миссию $$$(2, 3)$$$ с батареей емкости $$$c = 15$$$, используя путь $$$2 \rightarrow 7 \rightarrow 8 \rightarrow 9 \rightarrow 3$$$
| Название |
|---|




