У вас есть шахматная доска с $$$n$$$ рядами и $$$n$$$ столбцами. Изначально все клетки пусты, и в каждую из них вы должны поставить либо белого коня, либо черного коня.
Конь — шахматная фигура, которая может переместиться из клетки ($$$x_2$$$, $$$y_2$$$) в клетку ($$$x_1$$$, $$$y_1$$$), если одно из следующих условий выполняется:
- $$$|x_1 - x_2| = 2$$$ и $$$|y_1 - y_2| = 1$$$, или
- $$$|x_1 - x_2| = 1$$$ и $$$|y_1 - y_2| = 2$$$.
Ниже приведены примеры, как может ходить (и атаковать) конь. На каждой из нижеприведенных картинок, если конь находится в синей клетке, он атакует все красные клетки (и только их).
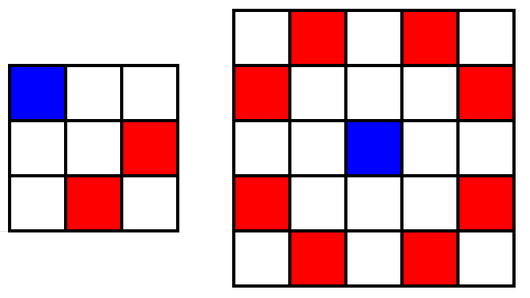
Дуэлью коней назовем пару коней разных цветов, атакующих друг друга. Вам нужно поставить коня (либо белого, либо черного) в каждую клетку так, чтобы количество дуэлей было максимально возможно.
В единственной строке задано одно целое $$$n$$$ ($$$3 \le n \le 100$$$) — количество рядов (и столбцов), из которых состоит шахматная доска.
Выведите $$$n$$$ строк, по $$$n$$$ символов в каждой. $$$j$$$-й символ в $$$i$$$-й строке должен быть W, если в клетке ($$$i$$$, $$$j$$$) должен стоять белый конь, или B, если в эту клетку нужно поставить черного коня. Количество дуэлей должно быть максимально возможным. Если оптимальных ответов несколько, выведите любой из них.
3
WBW BBB WBW
В первом примере $$$8$$$ дуэлей:
- белый конь в ($$$1$$$, $$$1$$$) атакует черного коня в ($$$3$$$, $$$2$$$);
- белый конь в ($$$1$$$, $$$1$$$) атакует черного коня в ($$$2$$$, $$$3$$$);
- белый конь в ($$$1$$$, $$$3$$$) атакует черного коня в ($$$3$$$, $$$2$$$);
- белый конь в ($$$1$$$, $$$3$$$) атакует черного коня в ($$$2$$$, $$$1$$$);
- белый конь в ($$$3$$$, $$$1$$$) атакует черного коня в ($$$1$$$, $$$2$$$);
- белый конь в ($$$3$$$, $$$1$$$) атакует черного коня в ($$$2$$$, $$$3$$$);
- белый конь в ($$$3$$$, $$$3$$$) атакует черного коня в ($$$1$$$, $$$2$$$);
- белый конь в ($$$3$$$, $$$3$$$) атакует черного коня в ($$$2$$$, $$$1$$$).
| Название |
|---|




