| Codeforces Round 580 (Div. 1) |
|---|
| Закончено |
Это интерактивная задача
Дано клетчатое поле $$$n\times n$$$, где $$$n$$$ нечетное. Строки пронумерованы от $$$1$$$ до $$$n$$$ сверху вниз, столбцы пронумерованы от $$$1$$$ до $$$n$$$ слева вправо. Клетка, стоящая на пересечении $$$x$$$-й строки и $$$y$$$-го столбца, будет обозначаться как $$$(x, y)$$$.
В каждой клетке записан $$$0$$$ или $$$1$$$. Известно, что в верхней левой клетке записана $$$1$$$, а в нижней правой записан $$$0$$$.
Мы хотим узнать, что записано в каждой клетке поля. Для этого мы можем задавать вопросы вида:
«$$$?$$$ $$$x_1$$$ $$$y_1$$$ $$$x_2$$$ $$$y_2$$$», где $$$1 \le x_1 \le x_2 \le n$$$, $$$1 \le y_1 \le y_2 \le n$$$, и $$$x_1 + y_1 + 2 \le x_2 + y_2$$$. Другими словами, мы выводим две различные клетки $$$(x_1, y_1)$$$, $$$(x_2, y_2)$$$ поля такие, что из первой можно добраться во вторую, идя только вправо и вниз, причем они не являются соседними.
В ответ на такой запрос вы узнаете, существует ли путь между $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$, идущий по клеткам только вправо или вниз, числа в клетках которого образуют палиндром.
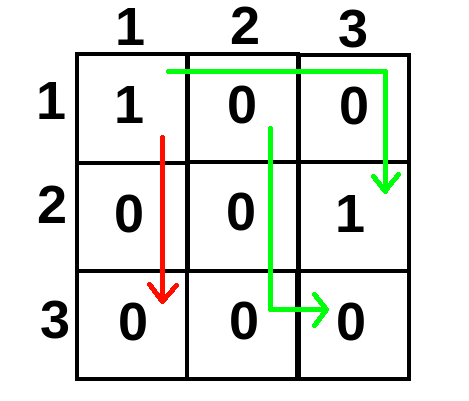
К примеру, пути, изображенные зеленым, являются палиндромными, поэтому ответ для «$$$?$$$ $$$1$$$ $$$1$$$ $$$2$$$ $$$3$$$» и «$$$?$$$ $$$1$$$ $$$2$$$ $$$3$$$ $$$3$$$» был бы, что такой путь существует. В то же время между точками $$$(1, 1)$$$ и $$$(3, 1)$$$ не существует палиндромного пути.
Определите все клетки поля, задав не более $$$n^2$$$ вопросов. Можно показать, что ответ всегда существует.
В первой строке находится нечетное целое число ($$$3 \le n < 50$$$) — сторона поля.
Вы начинаете взаимодействие, считав $$$n$$$.
Чтобы задать вопрос о клетках $$$(x_1, y_1), (x_2, y_2)$$$, в одной строке выведите «$$$?$$$ $$$x_1$$$ $$$y_1$$$ $$$x_2$$$ $$$y_2$$$».
Числа в запросе должны удовлетворять условиям $$$1 \le x_1 \le x_2 \le n$$$, $$$1 \le y_1 \le y_2 \le n$$$, и $$$x_1 + y_1 + 2 \le x_2 + y_2$$$. Не забудьте сделать операцию 'flush', чтобы получить ответ.
В ответ на заданный вопрос вы получите $$$1$$$, если существует путь идущий с $$$(x_1, y_1)$$$ в $$$(x_2, y_2)$$$ только вправо или вниз, числа в клетках которого образуют палиндром, и $$$0$$$ в противном случае.
В случае, если ваш запрос не соответствует требованиям, или вы задали более $$$n^2$$$ запросов, программа выведет $$$-1$$$ и прекратит взаимодействие. Вы получите вердикт Неправильный ответ. Вам нужно завершить работу вашей программы, чтобы не получить другие вердикты.
Когда вы установите все числа в клетках, выведите «!».
Далее выведите $$$n$$$ строк, $$$i$$$-я из которых — строка длины $$$n$$$, соответствующая числам в строке $$$i$$$ поля.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат для взломов
Чтобы взламывать, используйте следующий формат.
Первая строка должна содержать единственное нечетное число $$$n$$$ (сторона вашего поля).
$$$i$$$-я из $$$n$$$ последующих строчек должна содержать строку длины $$$n$$$ соответствующую $$$i$$$-й строке поля. Верхний левый элемент должен равняться $$$1$$$, нижний правый $$$0$$$.
3 0 1 0 1 1 1 1
? 1 1 1 3 ? 1 1 2 3 ? 2 1 2 3 ? 3 1 3 3 ? 2 2 3 3 ? 1 2 3 2 ? 1 2 3 3 ! 100 001 000
| Название |
|---|




