| Codeforces Round 576 (Div. 1) |
|---|
| Закончено |
Есть клетчатый квадрат размера $$$n \times n$$$. Некоторые клетки квадрата покрашены в черный цвет, остальные клетки покрашены в белый. За одну операцию разрешается выбрать некоторый прямоугольник и перекрасить все его клетки в белый цвет. За перекраску прямоугольника размера $$$h \times w$$$ взимается штраф в размере $$$\min(h, w)$$$. Требуется за минимальный суммарный штраф покрасить все клетки в белый цвет.
Квадрат большой, поэтому зададим мы его в сжатом виде. Множество чёрных клеток является объединением $$$m$$$ прямоугольников.
В первой строке ввода записаны два числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 10^{9}$$$, $$$0 \le m \le 50$$$) — размер квадрата и количество чёрных прямоугольников.
В следующих $$$m$$$ строках записаны по 4 числа $$$x_{i1}$$$ $$$y_{i1}$$$ $$$x_{i2}$$$ $$$y_{i2}$$$ ($$$1 \le x_{i1} \le x_{i2} \le n$$$, $$$1 \le y_{i1} \le y_{i2} \le n$$$) — координаты левой нижней и правой верхней клеток $$$i$$$-го чёрного прямоугольника.
Прямоугольники могут пересекаться.
Выведите одно число — минимальный суммарный штраф покраски всего квадрата в белый цвет.
10 2 4 1 5 10 1 4 10 5
4
7 6 2 1 2 1 4 2 4 3 2 5 2 5 2 3 5 3 1 2 1 2 3 2 5 3
3
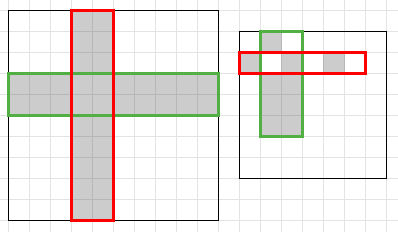
На картинке вы можете видеть два примера и некоторые из оптимальных способов их покрасить.
| Название |
|---|




