Назовем $$$k$$$-ступенчатой лестницей следующую конструкцию: ровно $$$k + 2$$$ деревянные доски, среди которых
- две доски длиной хотя бы $$$k+1$$$ — основные направляющие лестницы;
- $$$k$$$ досок длиной хотя бы $$$1$$$ — ступеньки лестницы.
Заметим, что ни направляющие, ни ступени не обязаны быть равны.
Например, лестницы $$$1$$$ и $$$3$$$ — корректные $$$2$$$-ступенчатые лестницы, а лестница $$$2$$$ — корректная $$$1$$$-ступенчатая. На первом изображении длины досок равны $$$[3, 3]$$$ для направляющих и $$$[1]$$$ для ступеньки. На втором изображении длины досок равны $$$[3, 3]$$$ для направляющих и $$$[2]$$$ для ступеньки. На третьем изображении длины досок равны $$$[3, 4]$$$ для направляющих и $$$[2, 3]$$$ для ступенек.
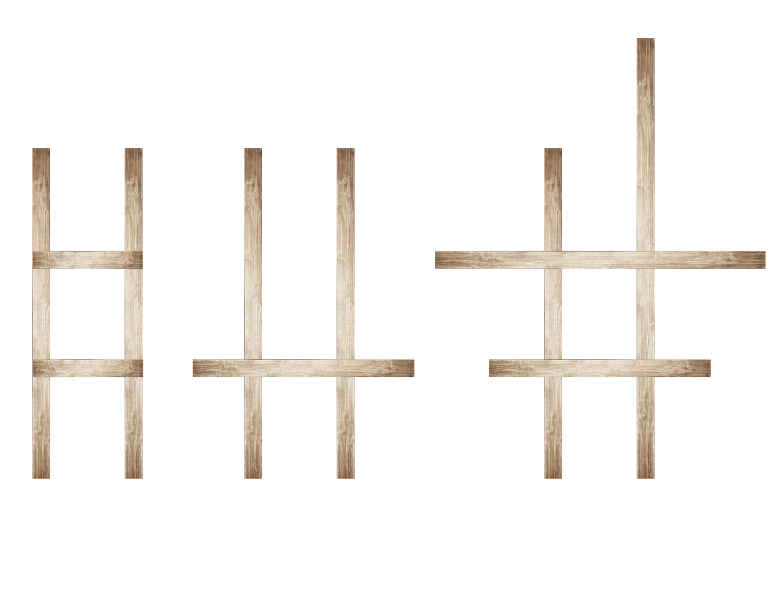
У вас есть $$$n$$$ досок. Длина $$$i$$$-й доски равна $$$a_i$$$. У вас нет пилы и вы не можете распиливать доски. Зато есть молоток и гвозди, и вы можете собрать импровизированную «лестницу» из тех досок, что есть.
Вопрос в следующем: чему равно максимальное $$$k$$$ такое, что вы сможете собрать $$$k$$$-ступенчатую лестницу, используя некоторый поднабор из имеющихся досок?
В первой строке задано единственное число $$$T$$$ ($$$1 \le T \le 100$$$) — количество запросов. Все запросы независимы.
Каждый запрос состоит из двух строк. В первой строке задано одно число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество досок у вас в наличии.
Во второй строке заданы $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^5$$$) — длины соответствующих досок.
Гарантируется, что суммарное количество досок во всех запросах не превосходит $$$10^5$$$.
Выведите $$$T$$$ чисел — по одному на запрос. $$$i$$$-е число обозначает максимальное $$$k$$$ такое, что вы можете собрать $$$k$$$-ступенчатую лестницу из досок описанных в $$$i$$$-м запросе.
Выведите $$$0$$$, если невозможно собрать даже $$$1$$$-ступенчатую лестницу из заданных досок.
4 4 1 3 1 3 3 3 3 2 5 2 3 3 4 2 3 1 1 2
2 1 2 0
Варианты лестниц для запросов $$$1-3$$$ представлены на картинке выше:
О качестве полученных лестниц:

| Название |
|---|




