There are $$$n$$$ segments drawn on a plane; the $$$i$$$-th segment connects two points ($$$x_{i, 1}$$$, $$$y_{i, 1}$$$) and ($$$x_{i, 2}$$$, $$$y_{i, 2}$$$). Each segment is non-degenerate, and is either horizontal or vertical — formally, for every $$$i \in [1, n]$$$ either $$$x_{i, 1} = x_{i, 2}$$$ or $$$y_{i, 1} = y_{i, 2}$$$ (but only one of these conditions holds). Only segments of different types may intersect: no pair of horizontal segments shares any common points, and no pair of vertical segments shares any common points.
We say that four segments having indices $$$h_1$$$, $$$h_2$$$, $$$v_1$$$ and $$$v_2$$$ such that $$$h_1 < h_2$$$ and $$$v_1 < v_2$$$ form a rectangle if the following conditions hold:
- segments $$$h_1$$$ and $$$h_2$$$ are horizontal;
- segments $$$v_1$$$ and $$$v_2$$$ are vertical;
- segment $$$h_1$$$ intersects with segment $$$v_1$$$;
- segment $$$h_2$$$ intersects with segment $$$v_1$$$;
- segment $$$h_1$$$ intersects with segment $$$v_2$$$;
- segment $$$h_2$$$ intersects with segment $$$v_2$$$.
Please calculate the number of ways to choose four segments so they form a rectangle. Note that the conditions $$$h_1 < h_2$$$ and $$$v_1 < v_2$$$ should hold.
The first line contains one integer $$$n$$$ ($$$1 \le n \le 5000$$$) — the number of segments.
Then $$$n$$$ lines follow. The $$$i$$$-th line contains four integers $$$x_{i, 1}$$$, $$$y_{i, 1}$$$, $$$x_{i, 2}$$$ and $$$y_{i, 2}$$$ denoting the endpoints of the $$$i$$$-th segment. All coordinates of the endpoints are in the range $$$[-5000, 5000]$$$.
It is guaranteed that each segment is non-degenerate and is either horizontal or vertical. Furthermore, if two segments share a common point, one of these segments is horizontal, and another one is vertical.
Print one integer — the number of ways to choose four segments so they form a rectangle.
7 -1 4 -1 -2 6 -1 -2 -1 -2 3 6 3 2 -2 2 4 4 -1 4 3 5 3 5 1 5 2 1 2
7
5 1 5 1 0 0 1 5 1 5 4 0 4 4 2 4 0 4 3 4 5
0
The following pictures represent sample cases:
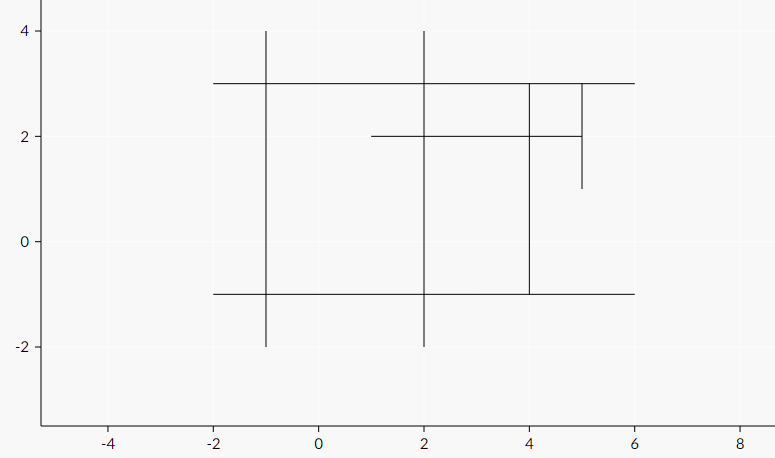
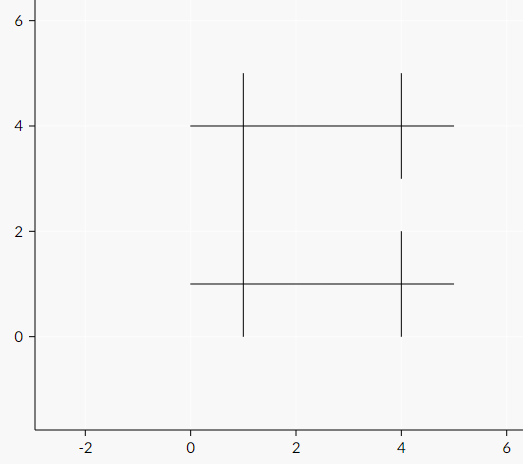
| Name |
|---|




