Вам дан кусочек бумаги в форме простого многоугольника $$$S$$$. Ваша задача — превратить его в простой многоугольник $$$T$$$, у которого такая же площадь, как у $$$S$$$.
У вас есть два инструмента: ножницы и скотч. Вы можете использовать ножницы, чтобы разрезать любой многоугольник на меньшие многоугольники. Скотч же можно использовать, чтобы склеить из меньших многоугольников большой. Каждый из инструментов можно использовать сколько угодно раз, в любом порядке.
Многоугольники, заданные вам, имеют целочисленные координаты, но вы можете получать части, которые имеют и нецелочисленные координаты.
Далее следует формальное описание задачи.
Фигурой $$$Q=(Q_0,\dots,Q_{n-1})$$$ называется последовательность из трех или более точек на плоскости такая, что:
- Замкнутая ломаная $$$Q_0Q_1Q_2\dots Q_{n-1}Q_0$$$ не имеет самокасаний и самопересечений, а поэтому образует простой многоугольник.
- Эта ломаная обходит многоугольник против часовой стрелки.
Обозначим многоугольник, ограниченный фигурой $$$Q$$$, за $$$P(Q)$$$.
Две фигуры называются эквивалентными, если одну из них можно перенести и повернуть так, чтобы она совпала со второй.
Обратите внимание, что отражать фигуры запрещено. Кроме того, обратите внимание, что порядок точек важен: фигура $$$(Q_1,\dots,Q_{n-1},Q_0)$$$ не всегда эквивалентна фигуре $$$(Q_0,\dots,Q_{n-1})$$$.
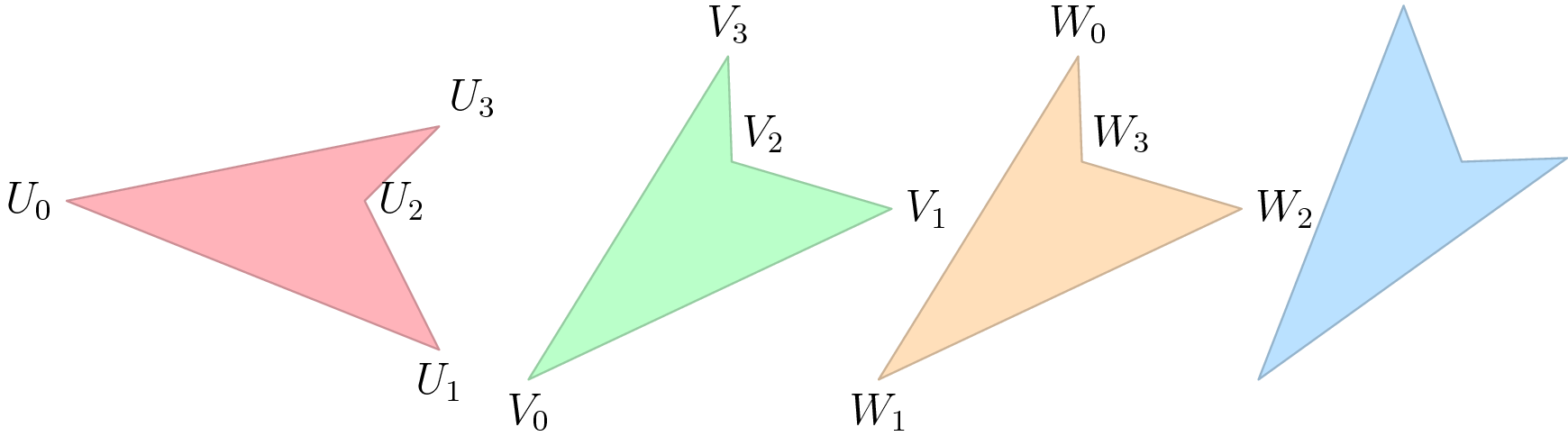
На рисунке слева: фигуры $$$U$$$ и $$$V$$$ эквивалентны. Фигура $$$W$$$ не эквивалентна им, потому что точки $$$W$$$ следуют в другом порядке. Четвертая фигура не эквивалентна остальным независимо от порядка точек, потому что отражение не допускается.
Во входных и выходных данных фигура из $$$n$$$ точек представляется как одна строка, содержащая $$$2n+1$$$ число: число $$$n$$$, а затем координаты точек: $$$Q_{0,x}$$$, $$$Q_{0,y}$$$, $$$Q_{1,x}$$$, ...
У фигур есть идентификационные номера (ID). Данная вам фигура $$$S$$$ имеет ID 0, фигуры, которые вы получаете в процессе решения — ID 1, 2, 3, ... в порядке, в которым вы их получаете.
Фигуры $$$B_1,\dots,B_k$$$ образуют разделение фигуры $$$A$$$, если:
- Объединение всех $$$P(B_i)$$$ дает точно $$$P(A)$$$.
- Для всех $$$i\neq j$$$ площадь пересечения $$$P(B_i)$$$ и $$$P(B_j)$$$ равна нулю.
Применение ножниц уничтожает одну существующую фигуру $$$A$$$ и создает одну или более фигуру $$$B_1,\dots,B_k$$$, которые образуют разделение $$$A$$$.
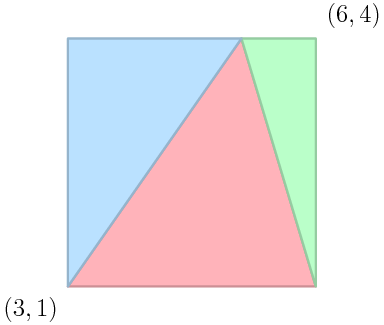
На рисунке фигура $$$A$$$ (квадрат) разделена на фигуры $$$B_1$$$, $$$B_2$$$, $$$B_3$$$ (три треугольника). Один из корректных способов представить одну из фигур $$$B_i$$$ есть «3 3 1 6 1 5.1 4».
Применение скотча уничтожает одну или более существующую фигуру $$$A_1,\dots,A_k$$$ и создает одну новую фигуру $$$B$$$. Чтобы эта операция была выполнима, вы должны в начале указать фигуры $$$C_1,\dots,C_k$$$, и только затем конечную фигуру $$$B$$$. Эти фигуры должны удовлетворять следующим ограничениям:
- Для всех $$$i$$$ фигура $$$C_i$$$ эквивалентна фигуре $$$A_i$$$.
- Фигуры $$$C_1,\dots,C_k$$$ образуют разделение фигуры $$$B$$$.
Неформально вы должны выбрать фигуру $$$B$$$ и показать, как нужно подвинуть и повернуть все существующие $$$A_i$$$, чтобы они заняли правильные места $$$C_i$$$ внутри $$$B$$$. Обратите внимание, что только фигура $$$B$$$ получает новый ID, фигуры $$$C_i$$$ его не получают.
Первая строка содержит исходную фигуру $$$S$$$.
Вторая строка содержит исходную фигуру $$$T$$$.
В обеих фигурах от 3 до 10 точек включительно. Обе фигуры даны в формате, описанном выше.
Все координаты во входных данных — целые числа в пределах от $$$-10^6$$$ до $$$10^6$$$ включительно.
В обеих фигурах никакие три точки не образуют угол меньший, чем 3 градуса. (Это утверждение включает в себя, в том числе, непоследовательные точки; кроме того, это означает, что никакие три точки не лежат на одной прямой.)
Многоугольники $$$P(S)$$$ и $$$P(T)$$$ имеют одинаковую площадь.
Каждый раз, когда вы используете ножницы, выведите блок строк в следующем виде:
scissors
id(A) k
B_1
B_2
...
B_k
Здесь $$$id(A)$$$ — ID фигуры, которую вы разрезаете, $$$k$$$ — число новых фигур, а $$$B_1,\dots,B_k$$$ — сами эти новые фигуры.
Каждый раз, когда вы используете скотч, выведите блок строк в следующем виде:
tape
k id(A_1) ... id(A_k)
C_1
C_2
...
C_k
B
Здесь $$$k$$$ — количество фигур, которые вы склеиваете, $$$id(A_1),\dots,id(A_k)$$$ — их ID, $$$C_1,\dots,C_k$$$ — их эквивалентные позиции внутри $$$B$$$, а $$$B$$$ — финальная фигура.
Рекомендуется выводить хотя бы 10 знаков после десятичной запятой.
Ваш вывод должен удовлетворять следующим условиям:
- Координаты всех точек должны быть в пределах от $$$-10^7$$$ до $$$10^7$$$ включительно.
- У всех фигур должно быть не более $$$100$$$ точек.
- В каждой операции число фигур $$$k$$$ должно быть в пределах от $$$1$$$ до $$$100$$$ включительно.
- Общее число операций не должно превышать $$$2000$$$.
- Общее число точек во всех фигурах не должно превышать $$$20000$$$.
- В конце должна быть ровно одна фигура (которая не была уничтожена), и эта фигура должна быть эквивалентна $$$T$$$.
- Все операции должны быть корректны. Решения с небольшими ошибками округления будут приняты. В проверяющей программе все проверки выполняются с абсолютной или относительной допустимой ошибкой в $$$10^{-3}$$$.
Фигура называется удобным прямоугольником, если она имеет вид $$$((0,0),~ (x,0),~ (x,y),~ (0,y))$$$ для некоторых положительных чисел $$$x$$$ и $$$y$$$.
Фигура называется удобным квадратом, если дополнительно $$$x=y$$$.
Фигура $$$A$$$ называется строго выпуклой, если все внутренние углы многоугольника $$$P(A)$$$ меньше 180 градусов.
Подзадача 1 (5 баллов): $$$S$$$ и $$$T$$$ — удобные прямоугольники. Все координаты точек — целые числа от 0 до 10 включительно
Подзадача 2 (13 баллов): $$$S$$$ — удобный прямоугольник с $$$x>y$$$, а $$$T$$$ — удобный квадрат
Подзадача 3 (12 баллов): $$$S$$$ и $$$T$$$ — удобные прямоугольники
Подзадача 4 (14 баллов): $$$S$$$ — треугольник, а $$$T$$$ — удобный квадрат
Подзадача 5 (10 баллов): $$$S$$$ и $$$T$$$ — треугольники
Подзадача 6 (16 баллов): $$$S$$$ — строго выпуклый многоугольник, а $$$T$$$ — удобный прямоугольник
Подзадача 7 (11 баллов): $$$T$$$ — удобный прямоугольник
Подзадача 8 (19 баллов): нет дополнительных ограничений
6 0 0 6 0 6 4 5 4 5 9 0 9 4 0 0 7 0 7 7 0 7
scissors 0 5 3 0 0 3 0 3 4 3 3 4 0 4 0 0 3 3 0 6 0 6 4 3 6 4 3 4 3 0 4 0 4 5 4 5 9 0 9 tape 5 1 2 5 3 4 3 0 3 0 0 4 0 3 4 0 7 0 7 4 4 0 3 4 0 7 4 3 7 3 7 4 7 7 3 7 3 3 7 0 7 0 3 4 0 0 7 0 7 7 0 7
4 0 0 3 0 3 3 0 3 4 7 -1 10 -1 11 2 8 2
scissors 0 2 3 0 0 1 3 0 3 4 1 3 0 0 3 0 3 3 tape 2 1 2 3 110 -1 111 2 110 2 4 108 2 107 -1 110 -1 110 2 4 107 -1 110 -1 111 2 108 2
4 0 0 9 0 9 1 0 1 4 0 0 3 0 3 3 0 3
scissors 0 2 4 1.470000000 0 9 0 9 1 1.470000000 1 4 0 0 1.470000000 0 1.470000000 1 0 1 scissors 1 2 4 1.470000000 0 6 0 6 1 1.470000000 1 4 9 0 9 1 6 1 6 0 tape 2 4 3 4 3 2 3 1 6 1 6 2 4 6 1 1.470000000 1 1.470000000 0 6 0 6 1.470000000 0 6 0 6 2 3 2 3 1 1.470000000 1 scissors 5 4 4 1.470000000 0 3 0 3 1 1.470000000 1 4 3 0 4 0 4 2 3 2 4 4 2 4 0 5 0 5 2 4 5 0 6 0 6 2 5 2 tape 5 2 6 7 8 9 4 0 0 1.470000000 0 1.470000000 1 0 1 4 1.470000000 0 3 0 3 1 1.470000000 1 4 0 2 0 1 2 1 2 2 4 0 2 2 2 2 3 0 3 4 3 3 2 3 2 1 3 1 4 0 0 3 0 3 3 0 3
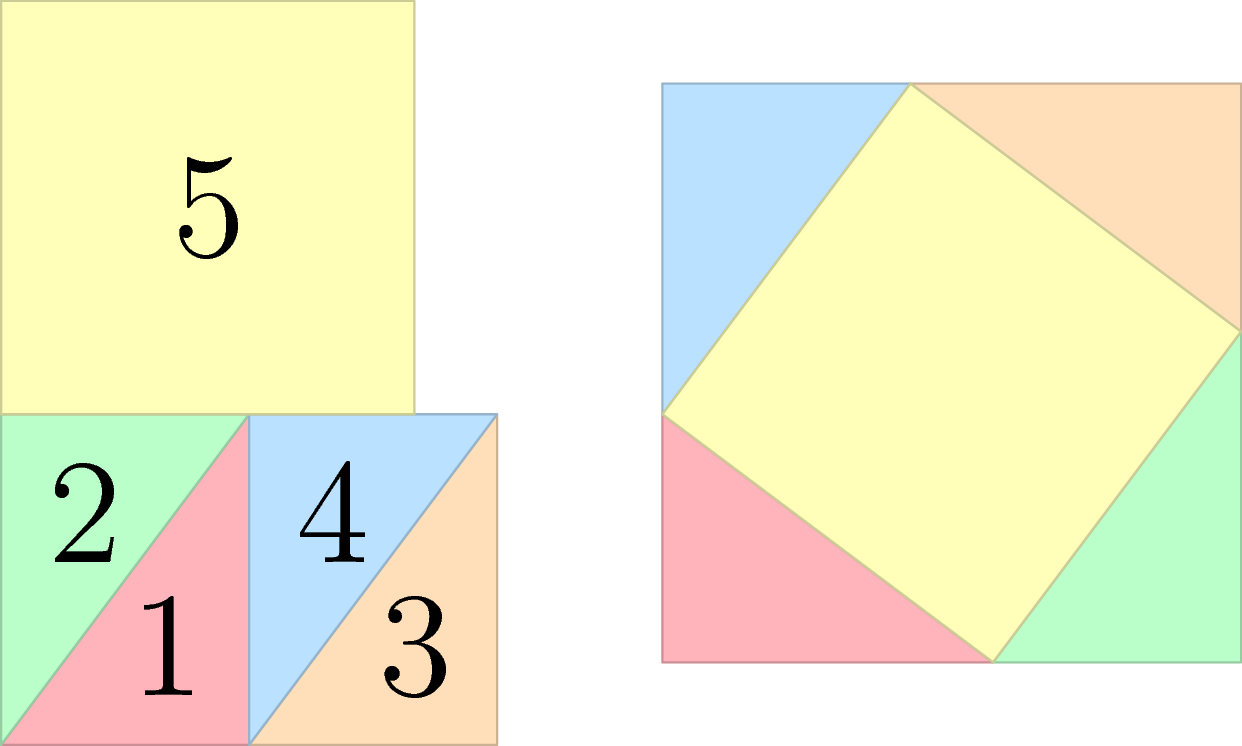
Рисунок ниже показывает ответ в первом примере. Слева показана изначальная фигура после использования ножниц, справа — соответствующие $$$C_i$$$, когда мы склеиваем все эти части обратно.
Во втором примере обратите, что достаточно, чтобы конечная фигура была идентична необходимой, они не обязательно должны быть идентичны.
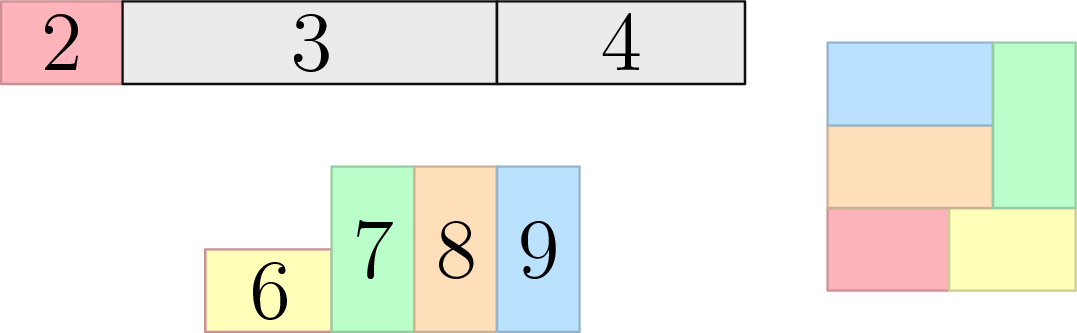
Рисунок ниже показывает три стадии получения результата в третьем примере. Сначала мы разрезаем исходный прямоугольник на два меньших, потом вы разрезаем больший из этих двух на еще два. Состояние после этого показано на верхнем левом рисунке.
Далее мы склеиваем два новых прямоугольника так, чтобы получился шестиугольник, и разрезаем этот многоугольник на три прямоугольника два на один и один меньший. Это показано на рисунке снизу слева.
Затем мы берем прямоугольник, который у нас все еще лежит с первого шага, и четыре меньших прямоугольника, и собираем из них желаемый квадрат три на три.
| Название |
|---|




