Кубворд — особый вид кроссворда. Для построения кубворда сначала выбирается положительное целое число $$$a$$$ — длина стороны куба. Затем строится большой куб, состоящий из $$$a \times a \times a$$$ единичных кубиков. У большого куба 12 ребер. После этого выкидываются все единичные кубики, которые не касаются ребер большого куба. Рисунок ниже показывает, что получится при $$$a=6$$$.
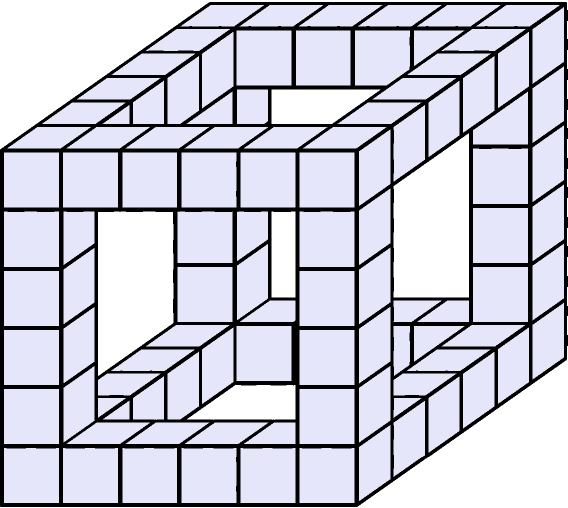
Наконец, вы пишете по одной букве в каждый единичный кубик. Вдоль каждого ребра большого куба должно получиться осмысленное слово. Буквы на любом ребре могут быть прочитаны в любом направлении, и достаточно, чтобы хотя бы в одном из направлений получилось осмысленное слово.
Рисунок ниже показывает фигуру при $$$a=6$$$, где в некоторые единичные кубики уже записаны буквы. Уже можно прочитать слова «SUBMIT», «ACCEPT» и «TURING» вдоль трех ребер большого куба.
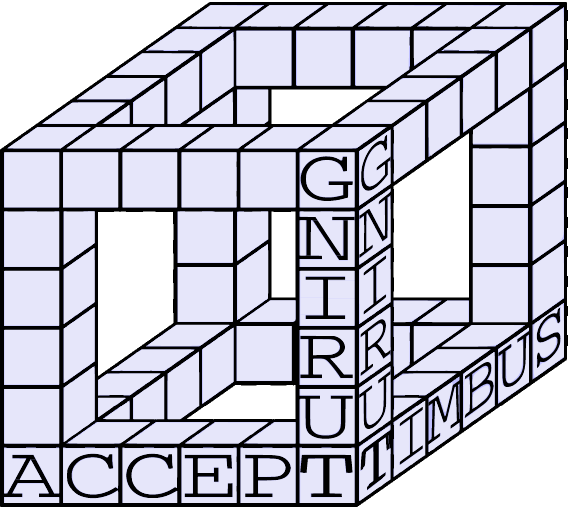
Вам дан список осмысленных слов. Каждое слово из этого списка может сколько угодно раз читаться на ребрах кубворда. Найдите число различных кубвордов, которые можно составить из этих слов, по модулю $$$998,244,353$$$.
Если один кубворд может быть получен из другого поворотом или отражением, они считаются различными.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 100,000$$$) – количество слов.
Далее следуют $$$n$$$ строк. Каждая из этих строк содержит одно слово, которое может присутствовать на ребрах большого куба. Длина каждого слова находится в пределах от 3 до 10 включительно.
Гарантируется, что все слова различны.
Выведите одно целое число — количество различных кубвордов из данных слов по модулю $$$998,244,353$$$.
Подзадача 1 (21 балл): слова содержат только буквы «a» - «f» (строчные)
Подзадача 2 (29 баллов): слова содержат только буквы «a» - «p» (строчные)
Подзадача 3 (34 балла): слова содержат только буквы «a» - «p» (строчные) и «A» - «P» (заглавные)
Подзадача 4 (16 баллов): слова содержат только буквы «a» - «z» (строчные), «A» - «Z» (заглавные) и цифры «0» - «9»
1 radar
1
1 robot
2
2 FLOW WOLF
2
2 baobab bob
4097
3 TURING SUBMIT ACCEPT
162
3 MAN1LA MAN6OS AN4NAS
114
В первом примере единственная возможность составить кубворд — написать слово «radar» на всех ребрах.
Во втором примере есть два различных кубворда, которые получаются друг из друга поворотом: слово «robot» на всех ребрах, и разница лишь в том, содержит ли левый нижний передний угол букву «r» или «t».
Третий пример похож на второй. То, что мы можем читать слова в обоих направлениях, не изменяет ответ.
В четвертом примере есть один кубворд со словом «bob» на каждом ребре. Кроме того, есть $$$2^{12} = 4096$$$ кубов со словом «baobab» на каждом ребре: для каждого из 12 ребер есть два возможных направления, в которых можно написать слово «baobab».
| Название |
|---|




