Вам дано взвешенное неориентированное дерево с $$$n$$$ вершинами, а также список из $$$q$$$ обновлений. Каждое обновление меняет вес одного ребра. Ваша задача — вычислить диаметр дерева после каждого обновления.
(Расстоянием между двумя вершинами называется сумма весов ребер на единственном простом пути между этими двумя вершинами. Диаметр дерева — наибольшее из этих расстояний.)
Первая строка содержит три разделенных пробелом целых числа $$$n$$$, $$$q$$$ и $$$w$$$ ($$$2 \leq n \leq 100,000, 1 \leq q \leq 100,000$$$, $$$1 \leq w \leq 20,000,000,000,000$$$) – число вершин в дереве, число обновлений и ограничение на вес ребер. Вершины пронумерованы от $$$1$$$ до $$$n$$$.
Следующие $$$n-1$$$ строк описывают изначальное дерево. $$$i$$$-я из этих строк содержит три целых числа $$$a_i$$$, $$$b_i$$$, $$$c_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$0 \leq c_i < w$$$), обозначающих, что изначально есть ребро между вершинами $$$a_i$$$ и $$$b_i$$$ с весом $$$c_i$$$. Гарантируется, что эти $$$n-1$$$ строк описывают дерево.
Последние $$$q$$$ строк описывают обновления. $$$j$$$-я из этих строк содержт два целых числа $$$d_j$$$, $$$e_j$$$ ($$$0 \leq d_j < n - 1, 0 \leq e_j < w$$$). Эти два числа вы должны изменить следующим образом:
- $$$d'_j = (d_j + last) \bmod (n - 1)$$$,
- $$$e'_j = (e_j + last) \bmod w$$$,
Выведите $$$q$$$ строк. Для всех возможных $$$i$$$ строка $$$i$$$ должна содержать диаметр дерева после $$$i$$$-го обновления.
Подзадача 1 (11 баллов): $$$n,q \leq 100$$$ и $$$w \leq 10,000$$$
Подзадача 2 (13 баллов): $$$n,q \leq 5,000$$$ и $$$w \leq 10,000$$$
Подзадача 3 (7 баллов): $$$w \leq 10,000$$$, и все ребра дерева имеют вид $$$\{1, i\}$$$ (То есть граф имеет вид «звезды» с центром в вершине 1.)
Подзадача 4 (18 баллов): $$$w \leq 10,000$$$, и все ребра дерева имеют вид $$$\{i, 2i\}$$$ и $$$\{i, 2i+1\}$$$ (То есть если мы подвесим дерево за вершину 1, то оно будет иметь вид сбалансированного бинарного дерева.)
Подзадача 5 (24 балла): гарантируется, что после каждого обновления по крайней мере один из наидлиннейших простых путей проходит через вершину $$$1$$$
Подзадача 6 (27 баллов): нет дополнительных ограничений
4 3 2000 1 2 100 2 3 1000 2 4 1000 2 1030 1 1020 1 890
2030 2080 2050
10 10 10000 1 9 1241 5 6 1630 10 5 1630 2 6 853 10 1 511 5 3 760 8 3 1076 4 10 1483 7 10 40 8 2051 5 6294 5 4168 7 1861 0 5244 6 5156 3 3001 8 5267 5 3102 8 3623
6164 7812 8385 6737 6738 7205 6641 7062 6581 5155
Первый пример показан на рисунке ниже. Рисунок слева показывает изначальное дерево. Каждый следующий рисунок показывает ситуацию после очередного обновления. Вес обновленного ребра показан зеленым, а диаметр — красным.
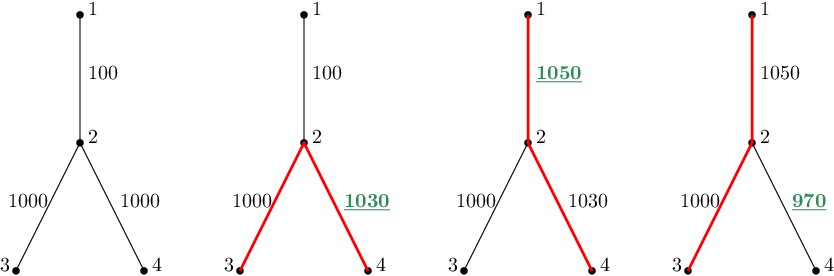
Первое обновление меняет вес $$$3$$$-го ребра, т.е. $$$\{2, 4\}$$$, на $$$1030$$$. Наибольшее расстояние между какой-либо парой вершин равно $$$2030$$$ — расстояние между $$$3$$$ и $$$4$$$.
Так как ответ равен $$$2030$$$, то для второго обновления $$$$$$d'_2 = (1 + 2030) \bmod 3 = 0$$$$$$ $$$$$$e'_2 = (1020 + 2030) \bmod 2000 = 1050$$$$$$ Поэтому вес ребра $$$\{1, 2\}$$$ меняется на $$$1050$$$. Теперь наибольшее расстояние между вершинами $$$\{1, 4\}$$$, оно равно $$$2080$$$.
Для третьего обновления имеем $$$$$$d'_3 = (1 + 2080) \bmod 3 = 2$$$$$$ $$$$$$e'_3 = (890 + 2080) \bmod 2000 = 970$$$$$$ Теперь, так как вес ребра $$$\{2, 4\}$$$ уменьшается до $$$970$$$, наиболее удаленная пара вершин, внезапно, $$$\{1, 3\}$$$, а расстояние — $$$2050$$$.
| Название |
|---|




