| Codeforces Global Round 4 |
|---|
| Закончено |
Это вторая подзадача задачи F. Единственные различия между этой и второй подзадачами — это ограничения на значение $$$m$$$ и ограничение по времени. Достаточно решить эту подзадачу, чтобы взламывать ее, но вам нужно решить обе подзадачи, чтобы взломать первую.
Во вселенной всего есть $$$n+1$$$ разных цветов, пронумерованных от $$$0$$$ до $$$n$$$. Есть полоска, длина которой $$$m$$$ сантиметров, изначально покрашенная в цвет $$$0$$$.
Алиса взяла кисть и начала разукрашивать полоску. Для каждого $$$i$$$ от $$$1$$$ до $$$n$$$ в таком порядке она выбирает два числа $$$0 \leq a_i < b_i \leq m$$$ такие, что отрезок $$$[a_i, b_i]$$$ сейчас покрашен одним цветом, и красит его в цвет $$$i$$$.
Алиса выбрала такие отрезки, что сейчас каждый сантиметр имеет отличный от $$$0$$$ цвет. Формально, отрезок $$$[i-1, i]$$$ покрашен в цвет $$$c_i$$$ ($$$c_i \neq 0$$$). Каждый цвет, кроме $$$0$$$, виден на полоске.
Посчитайте количество пар последовательностей $$$\{a_i\}_{i=1}^n$$$, $$$\{b_i\}_{i=1}^n$$$, которые дадут заданную полоску.
Так как это число может быть очень большим, выведите его по модулю $$$998244353$$$.
Первая строка содержит два целых числа $$$n$$$, $$$m$$$ ($$$1 \leq n \leq 500$$$, $$$n \leq m \leq 10^6$$$) — количество цветов, исключая цвет $$$0$$$, и длина полоски, соответственно.
Вторая строка содержит $$$m$$$ целых чисел $$$c_1, c_2, \ldots, c_m$$$ ($$$1 \leq c_i \leq n$$$) — цвет, который видно на отрезке $$$[i-1, i]$$$ после того, как раскраска закончилась. Гарантируется, что для каждого $$$j$$$ от $$$1$$$ до $$$n$$$ есть индекс $$$k$$$ такой, что $$$c_k = j$$$.
Выведите одно целое число — количество способов получить такую полоску по модулю $$$998244353$$$.
3 3 1 2 3
5
2 3 1 2 1
1
2 3 2 1 2
0
7 7 4 5 1 6 2 3 7
165
8 17 1 3 2 2 7 8 2 5 5 4 4 4 1 1 6 1 1
20
В первом примере всего есть $$$5$$$ способов, все они показаны на рисунке ниже. Здесь $$$0$$$ — белый цвет, $$$1$$$ — красный, $$$2$$$ — зеленый, а $$$3$$$ — синий.
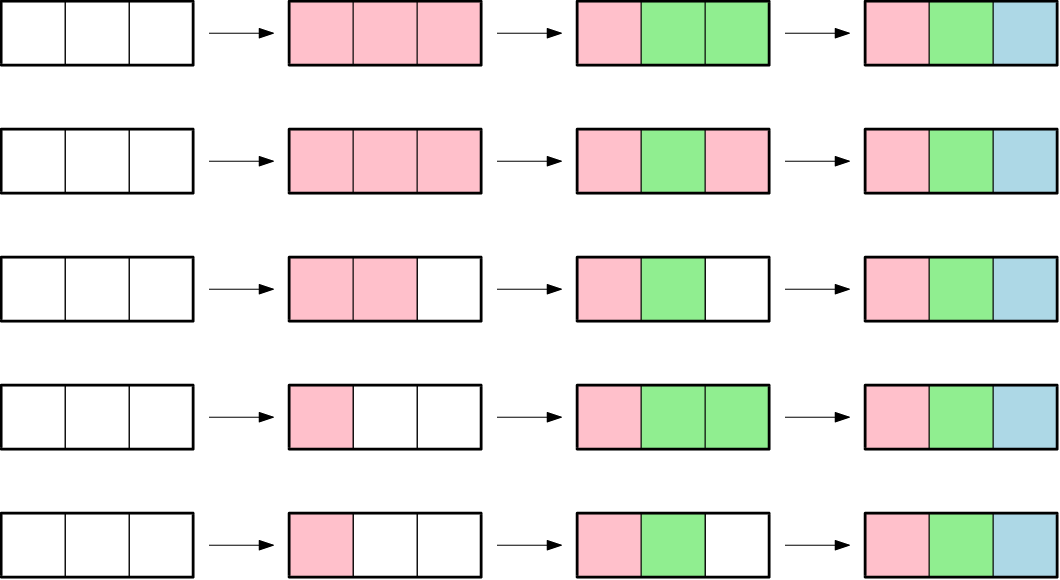
Ниже показан пример неправильной раскраски. Во второй операции отрезок 1 3 не покрашен ни в один цвет, поэтому он не может быть покрашен в цвет $$$2$$$.

Во втором примере, Алиса должна сначала покрасить отрезок 0 3 цветом $$$1$$$ и после этого отрезок 1 2 цветом $$$2$$$.
| Название |
|---|




