| Codeforces Global Round 4 |
|---|
| Закончено |
Все любят простые числа. Алиса тоже. Боб хотел вручить ей подарок, но не смог придумать ничего оригинального. Поэтому он решил подарить ей граф. Как изобретательно, Боб! Алисе точно понравится.
При построении графа Бобу нужно выполнить следующие четыре требования:
- Это должен быть простой неориентированный граф, то есть без петель и кратных (параллельных) ребер.
- Количество вершин должно быть ровно $$$n$$$ — число, которое выбрал Боб. Это число не обязательно простое.
- Количество ребер должно быть простым числом.
- Степень (т.е. количество рёбер, которые соприкасаются с вершиной) каждой вершины должна быть простым числом.
Ниже представлен пример для $$$n = 4$$$. Первый граф (слева) неправильный, так как степень вершины $$$2$$$ (так же как и $$$4$$$) равна $$$1$$$, а это число не является простым. Второй граф (посередине) неправильный, так как в нем $$$4$$$ ребра, что также не является простым числом. Третий граф (справа) правильный для $$$n = 4$$$.
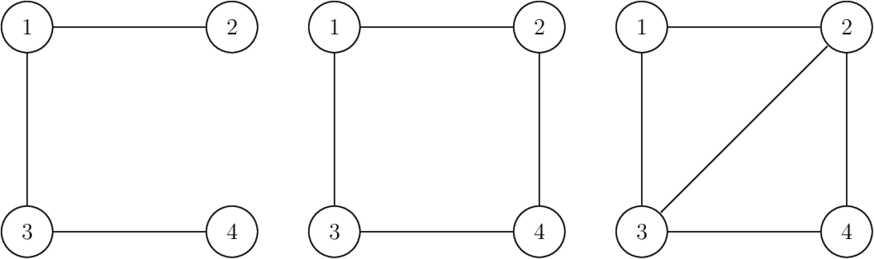
Обратите внимание, что граф может быть несвязным.
Пожалуйста, помогите Бобу найти любой такой граф!
Первая строка содержит одно целое число $$$n$$$ ($$$3 \leq n \leq 1\,000$$$) — количество вершин.
Если нет такого графа, для которого выполняются все условия, то выведите $$$-1$$$.
Иначе в первой строке выведите простое число $$$m$$$ ($$$2 \leq m \leq \frac{n(n-1)}{2}$$$) — количество ребер в графе. После этого выведите $$$m$$$ строк, в $$$i$$$-й из которых выведите два целых числа $$$u_i$$$, $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$), которые значат, что есть ребро между вершинами $$$u_i$$$ и $$$v_i$$$. Степень каждой вершины должна быть простым числом. Не должно быть петель и кратных (параллельных) ребер.
Если существует несколько решений, выведите любое из них.
Обратите внимание, что граф может быть несвязным.
4
5 1 2 1 3 2 3 2 4 3 4
8
13 1 2 1 3 2 3 1 4 2 4 1 5 2 5 1 6 2 6 1 7 1 8 5 8 7 8
Первый пример объяснен в легенде.
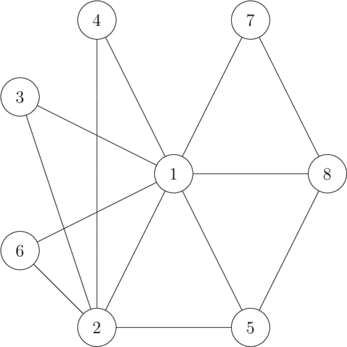
Во втором примере степени вершин равны $$$[7, 5, 2, 2, 3, 2, 2, 3]$$$. Каждое из этих чисел простое. Кроме того, количество ребер равно $$$13$$$, что тоже является простым числом, поэтому все условия выполнены.
| Название |
|---|




