| Codeforces Round 559 (Div. 1) |
|---|
| Закончено |
У Васи есть $$$n$$$ различных точек $$$A_1, A_2, \ldots A_n$$$ на плоскости. Никакие три из них не лежат на одной прямой. Он хочет расположить их в некотором порядке $$$A_{p_1}, A_{p_2}, \ldots, A_{p_n}$$$, где $$$p_1, p_2, \ldots, p_n$$$ — это некоторая перестановка чисел от $$$1$$$ до $$$n$$$.
Сделав так, он нарисует ориентированную ломаную на этих вершинах, проведя направленные отрезки из каждой точки в следующую в выбранном порядке точку. То есть для всех $$$1 \leq i \leq n-1$$$ он проведет направленный отрезок из точки $$$A_{p_i}$$$ в точку $$$A_{p_{i+1}}$$$. Он хочет, чтобы получившаяся ломаная удовлетворяла $$$2$$$-м условиям:
- она будет несамопересекающейся, то есть любые $$$2$$$ отрезка, которые не являются соседними, не имеют общих точек.
- она будет извилистой.
У Васи есть строка $$$s$$$, состоящая из $$$(n-2)$$$-х символов "L" или "R". Будем называть направленную ломаную извилистой, если её $$$i$$$-й поворот будет налево, если $$$s_i = $$$ "L" и направо, если $$$s_i = $$$ "R". Более формально: $$$i$$$-й поворот ломаной будет в точке $$$A_{p_{i+1}}$$$, в ней направленный отрезок из точки $$$A_{p_i}$$$ в точку $$$A_{p_{i+1}}$$$ поменяется на направленный отрезок из точки $$$A_{p_{i+1}}$$$ в точку $$$A_{p_{i+2}}$$$. Обозначим вектор $$$\overrightarrow{v_1} = \overrightarrow{A_{p_i} A_{p_{i+1}}}$$$ и вектор $$$\overrightarrow{v_2} = \overrightarrow{A_{p_{i+1}} A_{p_{i+2}}}$$$. Тогда если для того, чтобы повернуть вектор $$$\overrightarrow{v_1}$$$ на наименьший возможный угол, чтобы его направление совпало с направлением вектора $$$\overrightarrow{v_2}$$$ надо сделать поворот против часовой стрелки, то будем говорить, что $$$i$$$-й поворот налево, а иначе направо. Для лучшего понимания посмотрите картинки, на которых изображены различные варианты поворотов:
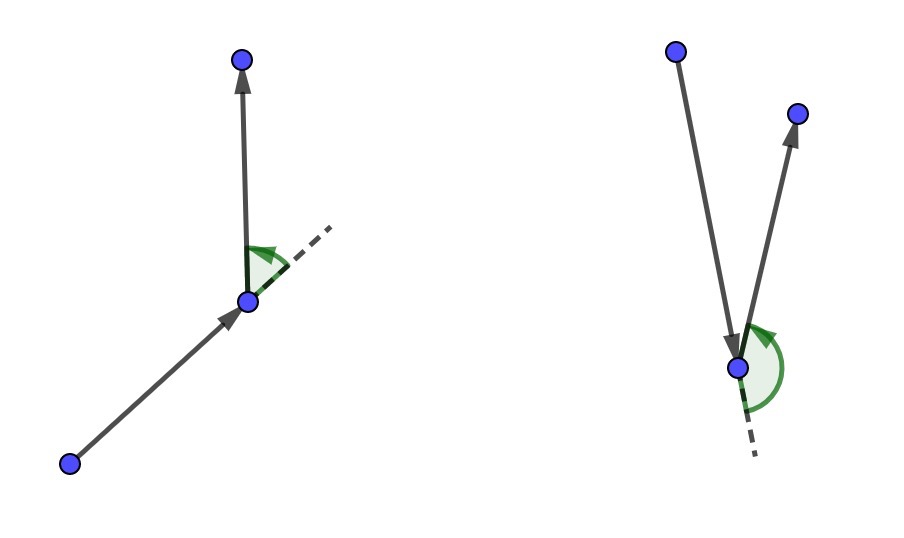 На этой картинке изображены повороты налево
На этой картинке изображены повороты налево 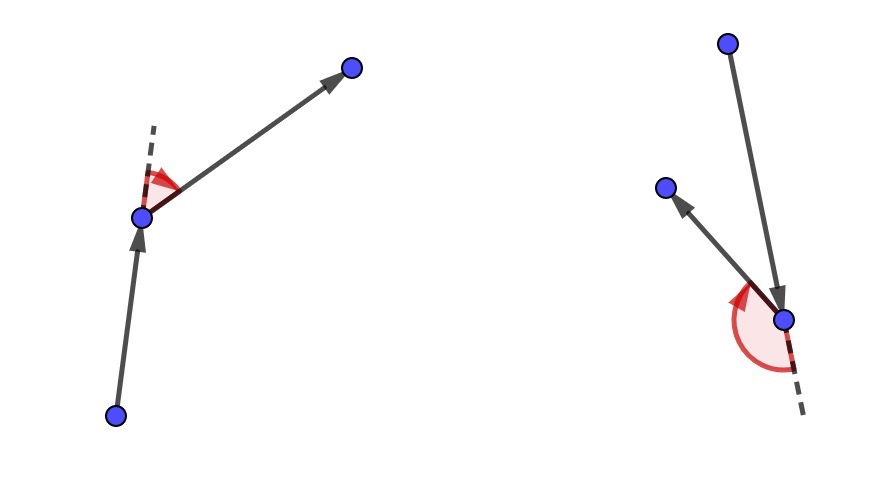 На этой картинке изображены повороты направо
На этой картинке изображены повороты направо Вам даны координаты точек $$$A_1, A_2, \ldots A_n$$$ на плоскости и строка $$$s$$$. Найдите перестановку $$$p_1, p_2, \ldots, p_n$$$ чисел от $$$1$$$ до $$$n$$$, такую что ломаная, которую нарисует Вася, будет удовлетворять двум заданным условиям.
В первой строке написано одно целое число $$$n$$$ — количество точек ($$$3 \leq n \leq 2000$$$). В следующих $$$n$$$ строках написаны по два целых числа $$$x_i$$$ и $$$y_i$$$, разделённые пробелом — координаты точки $$$A_i$$$ на плоскости ($$$-10^9 \leq x_i, y_i \leq 10^9$$$). В последней строке написана строка $$$s$$$ из символов "L" и "R" длины $$$(n-2)$$$. Гарантируется, что все точки различны и и никакие три точки не лежат на одной прямой.
Если подходящей перестановки не существует выведите $$$-1$$$. Иначе выведите $$$n$$$ чисел $$$p_1, p_2, \ldots, p_n$$$ — найденную перестановку ($$$1 \leq p_i \leq n$$$ и все $$$p_1, p_2, \ldots, p_n$$$ различны). Если подходящих перестановок несколько, выведите любую.
3 1 1 3 1 1 3 L
1 2 3
6 1 0 0 1 0 2 -1 0 -1 -1 2 1 RLLR
6 1 3 4 2 5
Вот картинка, изображающая ломаную из $$$1$$$ теста:
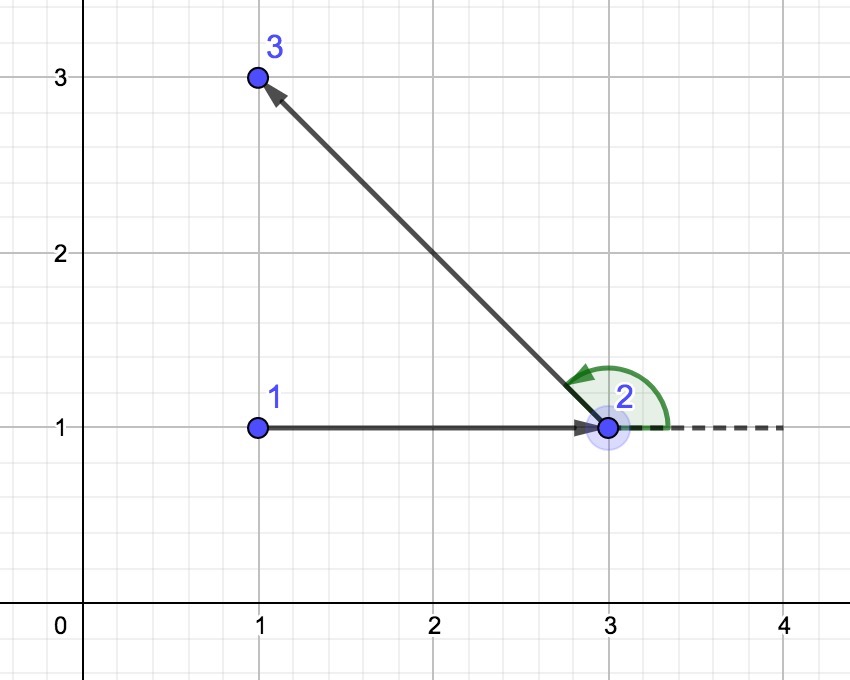
Как мы видим, эта ломаная несамопересекающаяся, а также извилистая, так как поворот в точке $$$2$$$ налево.
Вот картинка, изображающая ломаную из $$$2$$$ теста:
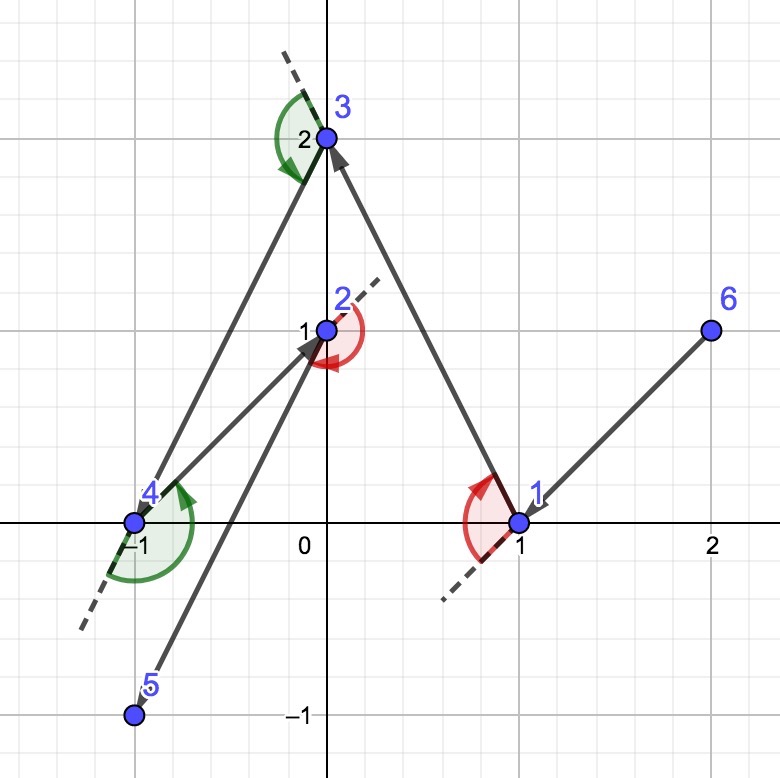
| Название |
|---|




