Задано дерево (неориентированный связный ацикличный граф), состоящее из $$$n$$$ вершин и $$$n - 1$$$ ребра. На каждом ребре записано число, каждое из чисел — это либо $$$0$$$ (назовем такие ребра $$$0$$$-ребрами), либо $$$1$$$ (назовем их $$$1$$$-ребрами).
Назовем упорядоченную пару вершин $$$(x, y)$$$ ($$$x \ne y$$$) корректной, если при проходе по простому пути от $$$x$$$ до $$$y$$$ мы никогда не пройдем по $$$0$$$-ребру после прохода по $$$1$$$-ребру. Ваша задача — посчитать количество корректных пар в дереве.
Первая строка входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 200000$$$) — количество вершин в дереве.
Затем следует $$$n - 1$$$ строка, каждая из которых описывает ребро дерева. Каждое ребро представлено в виде трех целых чисел $$$x_i$$$, $$$y_i$$$ и $$$c_i$$$ ($$$1 \le x_i, y_i \le n$$$, $$$0 \le c_i \le 1$$$, $$$x_i \ne y_i$$$) — вершины, соединенные этим ребром, и число, записанное на нем, соответственно.
Гарантируется, что заданный набор ребер формирует дерево.
Выведите одно целое число — количество корректных пар вершин.
7 2 1 1 3 2 0 4 2 1 5 2 0 6 7 1 7 2 1
34
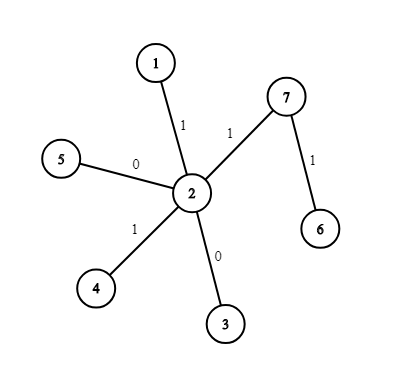
Картинка, соответствующая первому тестовому примеру:
| Название |
|---|




