Уровень математической подготовки абитуриентов математического факультета Берляндского Государственного Университета неожиданно резко упал. В этом году максимальный балл на вступительном экзамене по математике был 8. Из 100! Поэтому было принято решение упростить данный экзамен.
Теперь будущим студентам будут предлагать всего одну задачу. Задана последовательность целых чисел $$$a_1, a_2, \dots, a_n$$$, каждое число от $$$1$$$ до $$$3$$$, и $$$a_i \ne a_{i + 1}$$$ для всех корректных $$$i$$$. $$$i$$$-е число означает тип $$$i$$$-й фигуры:
- круг;
- равнобедренный треугольник, у которого длина высоты равна длине основания;
- квадрат.
Фигуры данной последовательности расположены где-то на плоскости с декартовой системой координат таким образом, что:
- $$$(i + 1)$$$-я фигура вписана в $$$i$$$-ю;
- основание каждого треугольника параллельно OX;
- треугольник ориентирован вершиной, лежащей напротив основания, наверх;
- стороны каждого квадрата параллельны осям координат;
- для каждого $$$i$$$ от $$$2$$$ до $$$n$$$ фигура $$$i$$$ имеет максимально возможную длину стороны, если это квадрат или треугольник, и максимально возможный радиус, если это круг.
Обратите внимание, что существует ровно одна конструкция для некоторых выбранных позиции и размера только первой фигуры.
Задача — посчитать количество различных точек (не обязательно имеющих целые координаты), где касаются фигуры. Хитрость, однако, в том, что это число иногда равно бесконечности. Но это же не усложнит вам задачу, правда?
Можете ли вы пройти тест и поступить в Берляндский Государственный Университет?
В первой строке записано одно целое число $$$n$$$ ($$$2 \le n \le 100$$$) — количество фигур.
Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 3$$$, $$$a_i \ne a_{i + 1}$$$) — типы фигур.
В первой строке выведите либо «Infinite», если количество различных точек, где касаются фигуры, бесконечно, и «Finite» в противном случае.
Если количество конечно, то выведите его во второй строке. Гарантируется, что данное число помещается в 32-битный тип целых чисел.
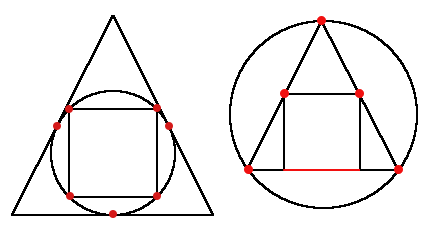
3 2 1 3
Finite 7
3 1 2 3
Infinite
Взгляните на эти потрясающие картинки для примеров. Обратите внимание, что треугольник не равносторонний, а просто равнобедренный и имеет длину высоты равной длине основания. Поэтому в квадрат он помещается единственным способом.
Различный точки, где касаются фигуры, отмечены красным.
Во втором примере треугольник и квадрат касаются на протяжении целого отрезка, он содержит бесконечное число точек.
| Название |
|---|




