Весь рынок доставки Берляндии находится под контролем у двух враждующих компаний: BerEx и BerPS. Обе компании предоставляют быструю и надежную доставку по всем городами Берляндии.
Карта Берляндии может быть представлена в виде неориентированного графа. Города — это вершины, а дороги — ребра, их соединяющие. Каждая пара городов соединена не более, чем одной дорогой. Каждая дорога соединяет различные города.
BerEx и BerPS соперничают настолько серьезно, что для каждой пары городов $$$(v, u)$$$ они установили свои маршруты из $$$v$$$ в $$$u$$$ таким образом, что эти два маршрута не имеют ни одной общей дороги. Гарантируется, что это было возможно.
Теперь правительство Берляндии решило урезать траты на поддержание дорог путем отказа от поддержания некоторых. Очевидно, они хотят поддерживать как можно меньше дорог. С другой стороны, они не хотят разрушить всю структуру доставок. То есть BerEx и BerPS должны сохранить возможность выбирать пути между каждой парой городов так, чтобы они не имели общих ребер.
Какое минимальное количество ребер правительство Берляндии может поддерживать?
Более формально, по заданному неориентированному реберно двусвязному графу сообщить минимальное число ребер, которое можно в нем оставить так, чтобы полученный граф тоже был реберно двусвязным.
В первой строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$3 \le n \le 14$$$, $$$n \le m \le \frac{n(n - 1)}{2}$$$) — количество городов и количество дорог между ними.
В каждой из следующих $$$m$$$ строк записаны по два целых числа $$$v$$$ и $$$u$$$ ($$$1 \le v, u \le n$$$, $$$v \ne u$$$) — города, соединенные очередной дорогой.
Гарантируется, что каждая пара городов соединена не более, чем одной дорогой. Гарантируется, что между каждой парой городов есть хотя бы два пути, которые не имеют общих ребер.
В первой строке выведите одно целое число $$$k$$$ – минимальное число дорог, которое правительство Берляндии может поддерживать так, чтобы у BerEx и BerPS оставалась возможность выбирать пути между каждой парой городов так, чтобы они не имели общих ребер.
Следующие $$$k$$$ строк должны содержать список дорог, которые будут поддерживаться. Каждая строка имеет вид "$$$v~u$$$", где $$$v$$$ и $$$u$$$ — это города, соединенные очередной дорогой.
Если существует несколько списков минимального размера, то выведите любой. Порядок дорог в списке не имеет значения.
3 3 1 2 2 3 3 1
3 1 3 3 2 1 2
4 5 1 2 1 4 2 3 4 3 1 3
4 1 4 4 3 3 2 1 2
6 10 1 2 2 3 3 1 3 4 4 5 5 6 4 6 2 5 1 6 3 5
6 1 6 6 5 5 4 4 3 3 2 1 2
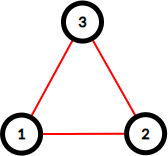
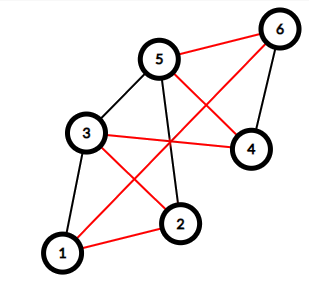
Здесь представлены графы из примеров, красные ребра значат дороги, которые поддерживаются.

| Название |
|---|




