B. Сервал и игрушечные кубики
ограничение по времени на тест
1 секунда
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

К счастью Сервалу повезло попасть на нужный автобус, и он успел приехать в детский сад вовремя. В детском саду ему сразу же понравились игрушечные кубики.

У него есть интересное хобби — придумывать разные задачки и давать их решать другим. В этот раз с помощью кубиков $$$1 \times 1 \times 1$$$ он построил трехмерную фигуру. Эту фигуру можно описать матрицей $$$n \times m$$$, что на клетке $$$(i,j)$$$ стоят друг на друге $$$h_{i,j}$$$ кубиков.

Сервал не расскажет вам $$$h_{i,j}$$$, он даст вам только вид спереди, вид слева, и вид сверху этой фигуры, и попросит вас восстановить фигуру. Вид спереди описывается $$$m$$$ столбцами, и высота $$$i$$$-го из них равна максимуму среди $$$h_{1,i},h_{2,i},\dots,h_{n,i}$$$. Аналогично описывается и вид слева, он задан $$$n$$$ столбцами. Вид сверху описывается матрицей $$$n \times m$$$ $$$t_{i,j}$$$, где $$$t_{i,j}$$$ равно $$$0$$$ или $$$1$$$. $$$t_{i,j}$$$, равное $$$1$$$, означает, что $$$h_{i,j}>0$$$, иначе $$$h_{i,j}=0$$$.

К сожалению, Сервалу очень одиноко, потому что все устали от его прошлых неразрешимых задач. Они отказываются решать эту даже несмотря на то, что в этот раз он обещает, что найдется хотя бы одна фигура, подходящая под все данные виды. Как его лучший друг, может быть, вы ее решите?

Входные данные

В первой строке записаны три положительных целых числа, разделенных пробелами $$$n, m, h$$$ ($$$1\leq n, m, h \leq 100$$$) — длина, ширина, и высота.

Во второй строке записаны $$$m$$$ неотрицательных целых чисел, разделенных пробелами, $$$a_1,a_2,\dots,a_m$$$, $$$a_i$$$ равно высоте $$$i$$$-го слева столбца в виде спереди ($$$0\leq a_i \leq h$$$).

В третьей строке записаны $$$n$$$ неотрицательных целых чисел, разделенных пробелами, $$$b_1,b_2,\dots,b_n$$$, $$$b_j$$$ равно высоте $$$j$$$-го слева столбца в виде слева ($$$0\leq b_j \leq h$$$).

В каждой из следующих $$$n$$$ строк записано по $$$m$$$ целых чисел, каждое из которых равно $$$0$$$ или $$$1$$$, описывающих матрицу. Если $$$h_{i, j}>0$$$, то $$$j$$$-е число в $$$i$$$-й строке равно $$$1$$$, и $$$0$$$ иначе.

Гарантируется, что существует хотя бы одна фигура, удовлетворяющая всем трем видам.

Выходные данные

Выведите $$$n$$$ строк, по $$$m$$$ целых чисел в каждой, $$$j$$$-е число в $$$i$$$-й строке должно быть равно высоте фигуры в соотвествующей позиции. Если существует несколько подходящих фигур, вы можете вывести любую.

Примеры
Входные данные
3 7 3
2 3 0 0 2 0 1
2 1 3
1 0 0 0 1 0 0
0 0 0 0 0 0 1
1 1 0 0 0 0 0
Выходные данные
1 0 0 0 2 0 0
0 0 0 0 0 0 1
2 3 0 0 0 0 0
Входные данные
4 5 5
3 5 2 0 4
4 2 5 4
0 0 0 0 1
1 0 1 0 0
0 1 0 0 0
1 1 1 0 0
Выходные данные
0 0 0 0 4
1 0 2 0 0
0 5 0 0 0
3 4 1 0 0
Примечание

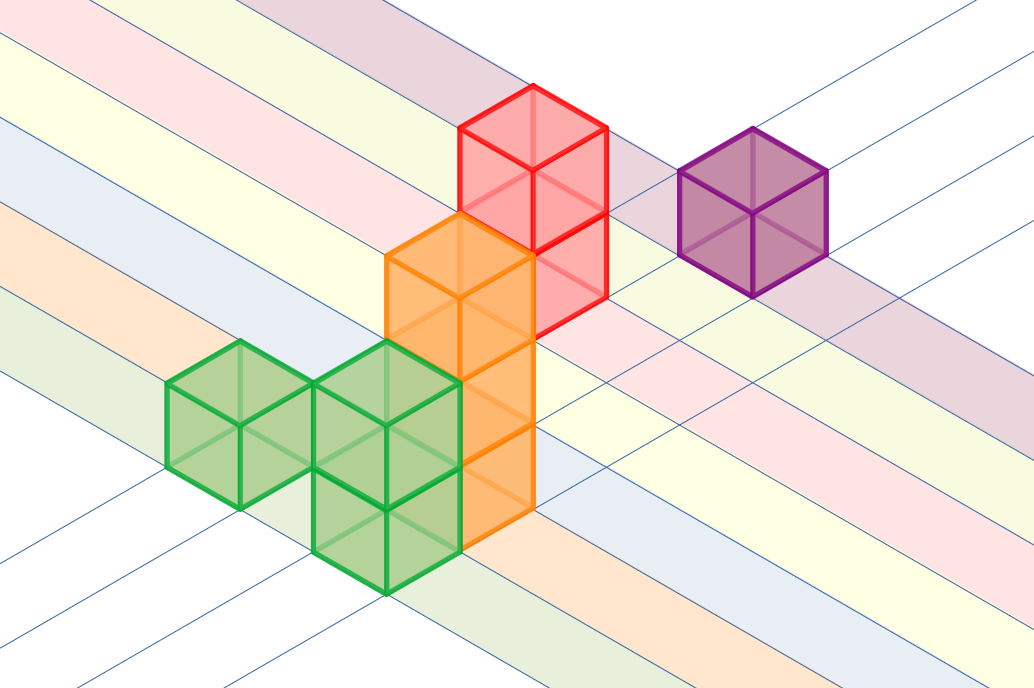
На приведенной выше иллюстрации изображена фигура из первого примера.

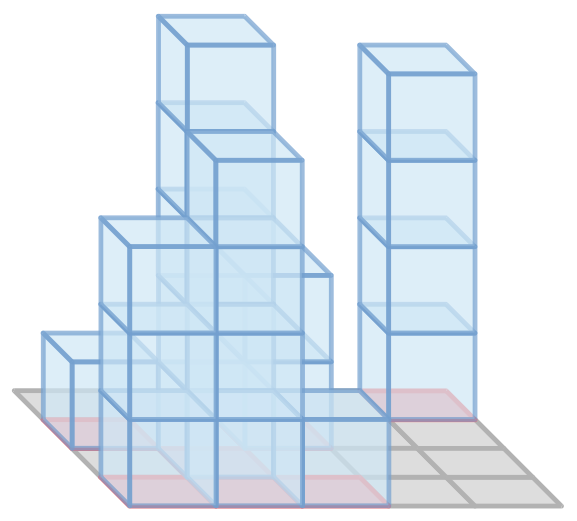
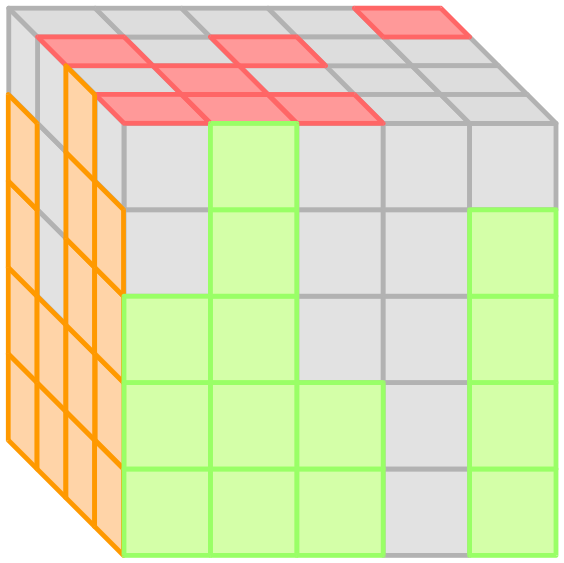
На первой из двух этих иллюстраций изображена фигура из второго примера, а на второй изображены три ее вида.