Вам дан набор из $$$n$$$ точек на 2D-плоскости. Гарантируется, что нет трех точек на одной прямой.
Пентаграмма — это набор из $$$5$$$ точек $$$A,B,C,D,E$$$, которые можно расположить следующим образом. 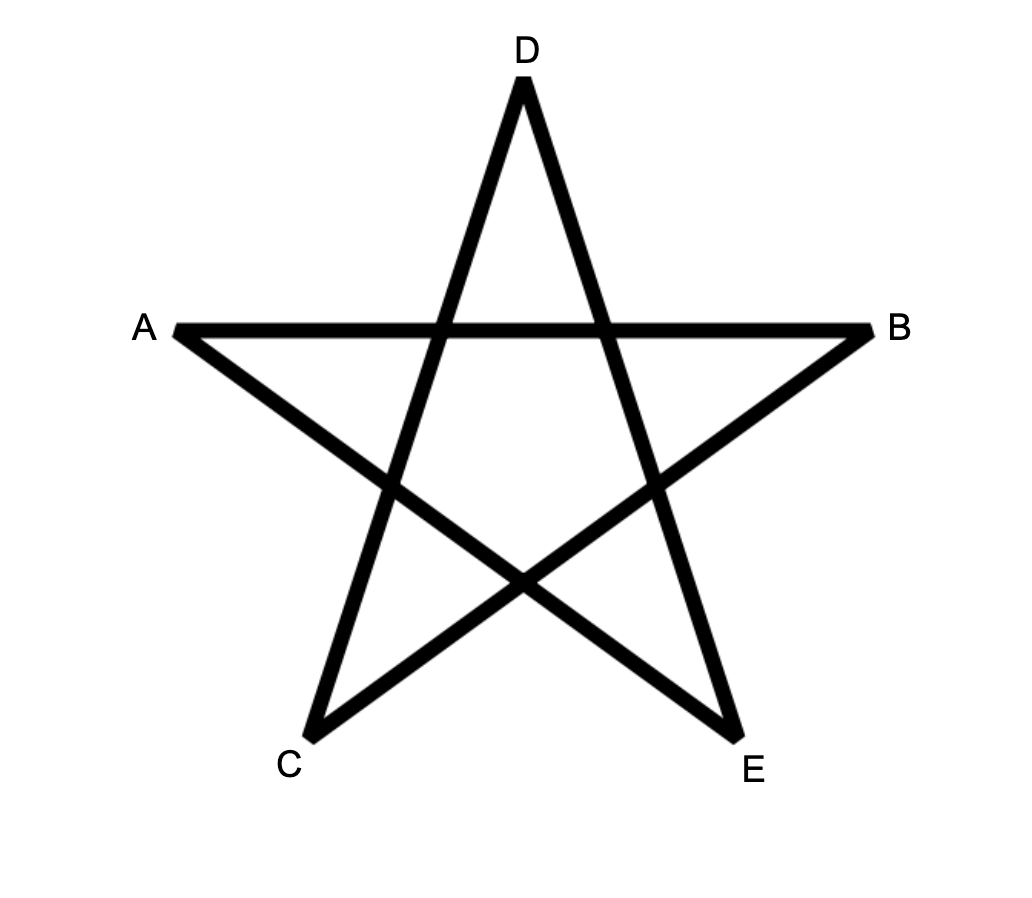 Обратите внимание, что длина отрезков не имеет значения, главное то, что пересечения существуют.
Обратите внимание, что длина отрезков не имеет значения, главное то, что пересечения существуют.
Подсчитайте количество способов выбрать $$$5$$$ точек из данного набора, которые образуют пентаграмму.
Первая строка содержит одно целое число $$$n$$$ ($$$5 \leq n \leq 300$$$) — количество точек.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_i, y_i$$$ ($$$-10^6 \leq x_i,y_i \leq 10^6$$$) — координаты $$$i$$$-й точки. Гарантируется, что нет трех точек на одной прямой.
Выведите одно целое число — количество множеств из $$$5$$$ точек, которые составляют пентаграмму.
5 0 0 0 2 2 0 2 2 1 3
1
5 0 0 4 0 0 4 4 4 2 3
0
10 841746 527518 595261 331297 -946901 129987 670374 -140388 -684770 309555 -302589 415564 -387435 613331 -624940 -95922 945847 -199224 24636 -565799
85
Первый пример:  Второй пример:
Второй пример:  Третий пример:
Третий пример: 
| Название |
|---|




