| Codeforces Round 550 (Div. 3) |
|---|
| Закончено |
Дан связный неориентированный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер. В заданном графе нет ни петель, ни кратных ребер.
Ориентируйте ребра графа таким образом, что в полученном ориентированном графе не будет путей, состоящих из двух или более ребер.
В первой строке заданы два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$n - 1 \le m \le 2 \cdot 10^5$$$) — количество вершин и ребер, соответственно.
Следующие $$$m$$$ строк задают ребра: ребро $$$i$$$ задается парой вершин $$$u_i$$$, $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$). В заданном графе нет кратных ребер, т. е. для каждой пары ($$$u_i, v_i$$$) не существует других пар ($$$u_i, v_i$$$) и ($$$v_i, u_i$$$) в списке ребер. Также гарантируется, что данный граф является связным (между любой парой вершин существует путь).
Если невозможно ориентировать ребра таким образом, что в графе не будет путей из двух или более ребер, выведите "NO" в первой строке.
Иначе в первой строке выведите "YES", а затем выведите любую подходящую ориентацию ребер в виде бинарной строки (строки, состоящей только из '0' и '1') длины $$$m$$$. $$$i$$$-й символ строки должен быть '0', если $$$i$$$-е ребро графа надо ориентировать из $$$u_i$$$ в $$$v_i$$$, и '1' в противном случае. Ребра пронумерованы в том же порядке, в котором заданы во входных данных.
6 5 1 5 2 1 1 4 3 1 6 1
YES 10100
Граф в первом примере из условия: 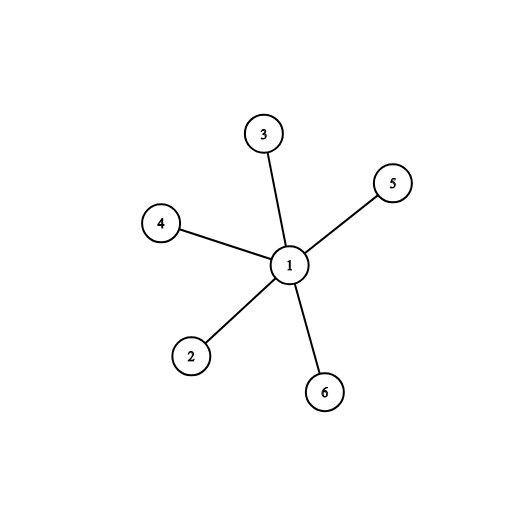
Один из возможных ответов: 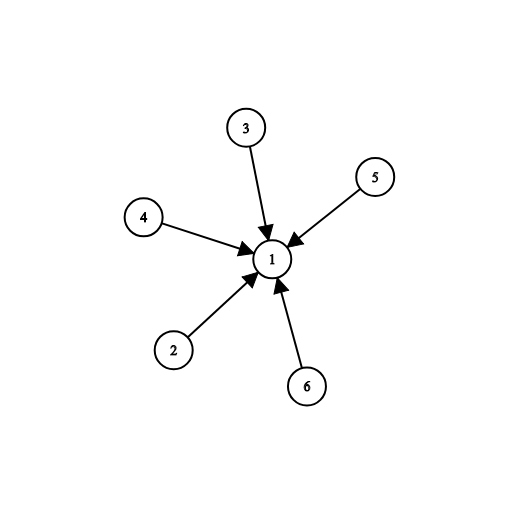
| Название |
|---|




