| Codeforces Round 545 (Div. 1) |
|---|
| Закончено |
Даша очень любит приключения. На днях ей встретился удивительный город, представляющий из себя $$$n$$$ улиц, направленных вдоль восточного направления, и $$$m$$$ улиц, направленных вдоль южного направления, образующих естественным образом $$$nm$$$ перекрестков. На любом пересечении $$$i$$$-й улицы, идущей на восток, и $$$j$$$-й улицы, идущей на юг, можно увидеть монументальной величины небоскреб. Загоревшись любопытством, Даша решила исследовать высоту городских строений.
Проходя через перекресток на пересечении $$$i$$$-й и $$$j$$$-й улицы соответствующих направлений, Даша оглядывает две улицы, на которых находится. Узнав высоты всех небоскрёбов, которые находятся на этих двух улицах, Даша задаётся вопросом: как можно переназначить высоты всем небоскрёбам на этих двух улицах, чтобы максимальная высота была как можно меньше, а результат сравнения высот у любых двух небоскрёбов на одной улице не изменился.
Сформулируем задачу формально. На каждом из $$$nm$$$ перекрёстков Даша независимо от других перекрёстков решает задачу. Сейчас она видит $$$n + m - 1$$$ небоскрёбов, и для каждого видит его настоящую высоту. При этом любые два небоскрёба можно сравнить по высоте и получить результат «больше», «меньше» или «равно». Теперь Даша хочет выбрать некоторое целое $$$x$$$, после чего назначить каждому небоскрёбу целую положительную высоту от $$$1$$$ до $$$x$$$. При назначении высот Даша хочет сохранить относительный порядок в каждой из улиц. То есть результат сравнения высоты любых двух небоскрёбов на текущей улице восточного направления не должен измениться, и результат сравнения высоты любых двух небоскрёбов на текущей улице южного направления не должен измениться. При этом небоскрёбы, находящиеся только на текущей улице восточного направления не сравниваются с небоскрёбами, находящими на текущей улице южного направления, а небоскрёб, находящийся на пересечении, может сравниваться и с теми и с теми. Для каждого перекрёстка Даша хочет независимо вычислить минимальное возможное подходящее $$$x$$$.
Например, если выбранный перекрёсток и улицы ему соответствующие выглядят следующим образом:
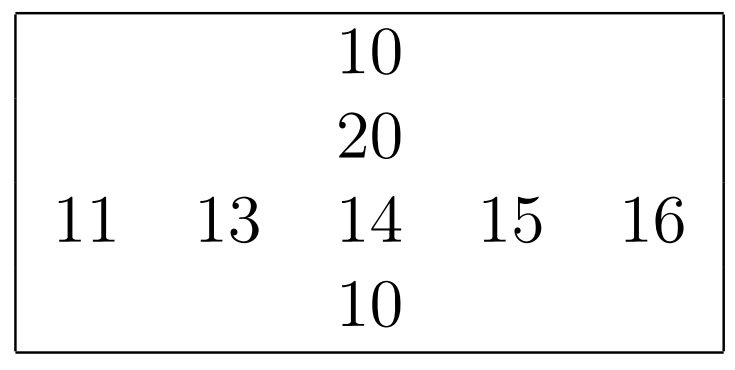
То можно заменить высоты небоскрёбов следующим образом (заметим, что все сравнения на меньше, больше или равно внутри улицы южного направления и внутри улицы восточного направления при этом не поменяются).
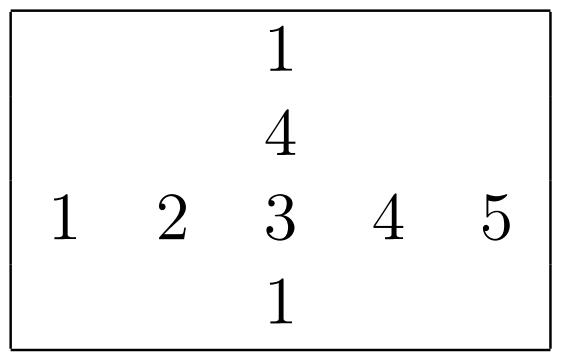
Наибольшее использованное число равно $$$5$$$, а значит ответом для этого перекрёстка было бы $$$5$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 1000$$$) — количество улиц, идущих вдоль восточного направления и южного соответственно.
Каждая из следующих $$$n$$$ содержит по $$$m$$$ целых чисел $$$a_{i,1}$$$, $$$a_{i,2}$$$, ..., $$$a_{i,m}$$$ ($$$1 \le a_{i,j} \le 10^9$$$) в каждой. Число $$$a_{i,j}$$$, находящееся на $$$j$$$-й позиции в $$$i$$$-й строке, характеризует высоту небоскреба, находящегося на пересечении $$$i$$$-й улицы восточного направления и $$$j$$$-й улицы южного направления.
Выведите $$$n$$$ строк, по $$$m$$$ целых положительных чисел, где число $$$x_{i,j}$$$, находящееся на $$$j$$$-й позиции в $$$i$$$-й строке — это ответ на задачу в перекрестке на пересечении $$$i$$$-й улицы восточного направления и $$$j$$$-й улицы южного направления.
2 3 1 2 1 2 1 2
2 2 2 2 2 2
2 2 1 2 3 4
2 3 3 2
В первом примере из условия ни на одном из перекрестков максимальную высоту уменьшить не получится, а значит можно просто не менять высоты.
Во втором примере из условия имеем следующие ответы:
- Для пересечения первой строки и первого столбца:
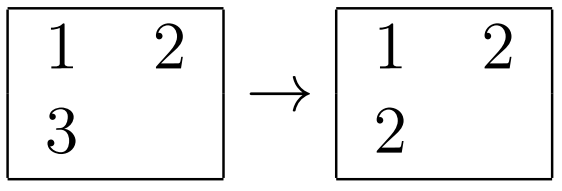
- Для пересечения первой строки и второго столбца:
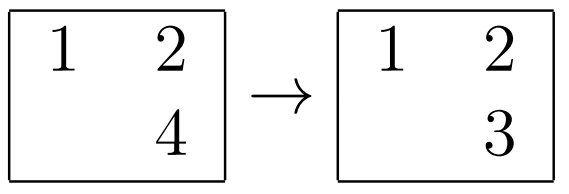
- Для пересечения второй строки и первого столбца:
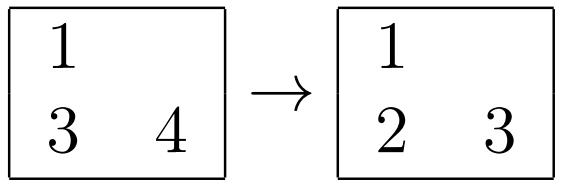
- Для пересечения второй строки и второго столбца:
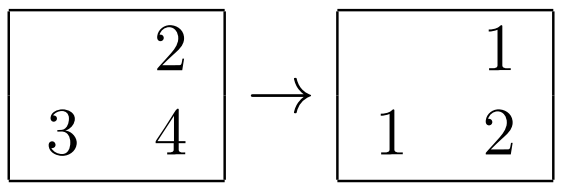
| Название |
|---|




