| Codeforces Round 546 (Div. 2) |
|---|
| Закончено |
Настя пришла в школу на урок информатики, и известный в узких кругах учитель, который в данный момент преподает у Насти, задал ей такую задачу.
Даны две матрицы $$$A$$$ и $$$B$$$, каждая размера $$$n \times m$$$. Настя может сколько угодно раз применять к матрице $$$A$$$ следующую операцию: взять любую квадратную подматрицу матрицы $$$A$$$ и транспонировать её (то есть элемент подматрицы, стоявший в $$$i$$$-й строке и $$$j$$$-м столбце этой подматрицы, после операции транспонирования будет стоять в ней в $$$j$$$-й строке и в $$$i$$$-м столбце, при этом сама подматрица в уже транспонированном виде останется на том же месте в матрице $$$A$$$). Требуется ответить, можно ли из матрицы $$$A$$$ получить матрицу $$$B$$$.
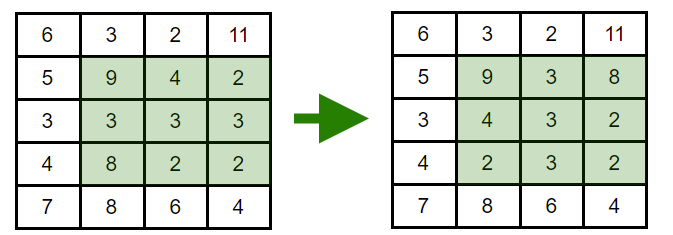 Пример описанной операции
Пример описанной операции Так как Настя не хочет выполнять эти операции вручную, она просит вас ответить на этот вопрос.
Квадратной подматрицей матрицы $$$M$$$ называется матрица, образованная элементами на пересечении множества строк с номерами $$$x, x+1, \dots, x+k-1$$$ матрицы $$$M$$$ и множества столбцов с номерами $$$y, y+1, \dots, y+k-1$$$ матрицы $$$M$$$, где $$$k$$$ — размер квадратной подматрицы. Иными словами, квадратная подматрица — это набор ячеек исходной матрицы, которые образуют сплошной (без пустот) квадрат со сторонами параллельными сторонам исходной матрицы.
В первой строке вводятся два целых числа $$$n$$$ и $$$m$$$, разделенных пробелом ($$$1 \leq n, m \leq 500$$$) — количество строк и столбцов в матрицах $$$A$$$ и $$$B$$$ соответственно.
В следующих $$$n$$$ строках вводятся по $$$m$$$ целых чисел, разделенных пробелом: $$$j$$$-е число в $$$i$$$-й из этих строк обозначает $$$j$$$-й элемент $$$i$$$-й строки матрицы $$$A$$$ ($$$1 \leq A_{ij} \leq 10^{9}$$$).
В следующих $$$n$$$ строках вводятся по $$$m$$$ целых чисел, разделенных пробелом: $$$j$$$-е число в $$$i$$$-й из этих строк обозначает $$$j$$$-й элемент $$$i$$$-й строки матрицы $$$B$$$ ($$$1 \leq B_{ij} \leq 10^{9}$$$).
Выведите «YES» (без кавычек), если вышеуказанными действиями можно превратить матрицу $$$A$$$ в матрицу $$$B$$$, и «NO» (без кавычек), если нельзя.
2 2 1 1 6 1 1 6 1 1
YES
2 2 4 4 4 5 5 4 4 4
NO
3 3 1 2 3 4 5 6 7 8 9 1 4 7 2 5 6 3 8 9
YES
Рассмотрим третий пример из условия. Изначальная матрица $$$A$$$ имеет вид
$$$$$$ \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} $$$$$$
Если выбрать как транспонируемую квадратную подматрицу всю матрицу, то после транспонирования получим
$$$$$$ \begin{bmatrix} 1 & 4 & 7\\ 2 & 5 & 8\\ 3 & 6 & 9 \end{bmatrix} $$$$$$
Теперь транспонируем матрицу с углами в клетках $$$(2, 2)$$$ и $$$(3, 3)$$$.
$$$$$$ \begin{bmatrix} 1 & 4 & 7\\ 2 & \textbf{5} & \textbf{8}\\ 3 & \textbf{6} & \textbf{9} \end{bmatrix} $$$$$$
Получим
$$$$$$ \begin{bmatrix} 1 & 4 & 7\\ 2 & 5 & 6\\ 3 & 8 & 9 \end{bmatrix} $$$$$$
что, в свою очередь, и есть матрица $$$B$$$.
| Название |
|---|




