| Codeforces Global Round 2 |
|---|
| Закончено |
Недавно Алена купила миниатюрный холодильник, который может быть представлен как таблица из $$$h$$$ строк и $$$2$$$ столбцов. Изначально в холодильнике лишь одна полка в самом низу, но Алена может установить любое число полок внутрь холодильника между любыми двумя рядами. Все полки имеют ширину в две клетки, не занимают места по вертикали, но разделяют холодильник на верхнюю и нижнюю части.
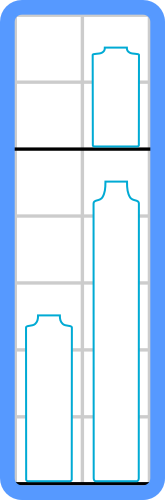 Пример холодильника с $$$h = 7$$$ и двумя полками. Полки показаны черным. Рисунок соответствует первому примеру.
Пример холодильника с $$$h = 7$$$ и двумя полками. Полки показаны черным. Рисунок соответствует первому примеру. У Алены есть $$$n$$$ бутылок молока, она хочет поставить их в холодильник. Высота $$$i$$$-й бутылки равна $$$a_i$$$ клеток, а ширина любой бутылки равна $$$1$$$ клетке. Алена может поставить бутылку на полку, если высота свободного пространства над этой полкой не меньше высоты бутылки. Она не может ставить бутылки друг на друга (если, конечно, между ними нет полки). Бутылки не могут занимать общие клетки в таблице.
Алена хочет найти максимальное целое число $$$k$$$ такое, что она может одновременно поставить бутылки с номерами $$$1$$$, $$$2$$$, ..., $$$k$$$ в холодильник. Найдите это наибольшее $$$k$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$h$$$ ($$$1 \le n \le 10^3$$$, $$$1 \le h \le 10^9$$$) — количество бутылок и высота холодильника, соответственно.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1$$$, $$$a_2$$$, ..., $$$a_n$$$ ($$$1 \le a_i \le h$$$) — высоты бутылок.
Выведите одно целое число $$$k$$$ — максимальное целое число такое, что Алена может одновременно поставить бутылки с номерами $$$1$$$, $$$2$$$, ..., $$$k$$$ в холодильник. Если Алена может поставить все бутылки, выведите $$$n$$$. Легко понять, что Алена всегда может поставить хотя бы одну бутылку в холодильник.
5 7 2 3 5 4 1
3
10 10 9 1 1 1 1 1 1 1 1 1
4
5 10 3 1 4 2 4
5
Один из оптимальных способов постановки бутылок в холодильник в первом примере показан на рисунке в условии.
Один из оптимальных способов постановки бутылок в холодильник во втором примере показан на рисунке ниже.

Один из оптимальных способов постановки бутылок в холодильник во третьем примере показан на рисунке ниже.

| Название |
|---|




