| Codeforces Round 535 (Div. 3) |
|---|
| Закончено |
Задан неориентированный взвешенный связный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер без петель и кратных ребер.
$$$i$$$-е ребро — $$$e_i = (u_i, v_i, w_i)$$$; расстояние между вершинами $$$u_i$$$ и $$$v_i$$$ по ребру $$$e_i$$$ равно $$$w_i$$$ ($$$1 \le w_i$$$). Граф является связным, то есть для каждой пары вершин существует хотя бы один путь между ними, состоящий только из ребер заданного графа.
Минимальное остовное дерево (MST) в случае положительных весов — это подмножество ребер связного взвешенного неориентированного графа, соединяющее все его вершины и имеющее минимальный суммарный вес среди всех таких подмножеств (суммарный вес — это сумма весов выбранных ребер).
Вы можете модифицировать заданный граф. Единственная операция, которую вы можете проводить, заключается в следующем: увеличить вес какого-либо ребра на $$$1$$$. Вы можете увеличивать вес каждого ребра любое (возможно, нулевое) количество раз.
Предположим, что изначальный вес MST был равен $$$k$$$. Ваша задача — увеличить веса некоторых ребер за минимально возможное количество операций таким образом, чтобы вес MST в получившемся графе остался равен $$$k$$$, но MST стало уникальным (это означает, что есть только один способ выбрать MST в получившемся графе).
Ваша задача — посчитать минимальное количество операций, необходимое для того, чтобы это сделать.
Первая строка входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 2 \cdot 10^5, n - 1 \le m \le 2 \cdot 10^5$$$) — количество вершин и количество ребер в изначальном графе.
The next $$$m$$$ строк содержат по три целых числа. $$$i$$$-я строка содержит описание $$$i$$$-го ребра $$$e_i$$$. Оно определяется тремя целыми числами $$$u_i, v_i$$$ и $$$w_i$$$ ($$$1 \le u_i, v_i \le n, u_i \ne v_i, 1 \le w \le 10^9$$$), где $$$u_i$$$ и $$$v_i$$$ — вершины, соединяемые $$$i$$$-м ребром, а $$$w_i$$$ — вес этого ребра.
Гарантируется, что заданный граф не содержит петель и кратных ребер (то есть для каждого $$$i$$$ от $$$1$$$ до $$$m$$$ $$$u_i \ne v_i$$$ и для каждой неориентированной пары $$$(u, v)$$$ существует не более одного ребра, соединяющего эту пару вершин). Также гарантируется, что заданный граф является связным.
Выведите одно целое число — минимальное количество операций, чтобы унифицировать MST заданного графа без изменения веса MST.
8 10 1 2 1 2 3 2 2 4 5 1 4 2 6 3 3 6 1 3 3 5 2 3 7 1 4 8 1 6 2 4
1
4 3 2 1 3 4 3 4 2 4 1
0
3 3 1 2 1 2 3 2 1 3 3
0
3 3 1 2 1 2 3 3 1 3 3
1
1 0
0
5 6 1 2 2 2 3 1 4 5 3 2 4 2 1 4 2 1 5 3
2
Картинка, соответствующая первому тестовому примеру: 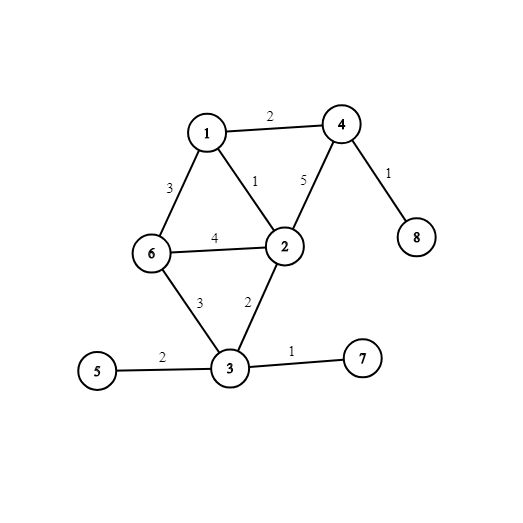
Вы можете, например, увеличить вес ребра $$$(1, 6)$$$ или $$$(6, 3)$$$ на $$$1$$$ для унификации MST.
Картинка, соответствующая последнему тестовому примеру: 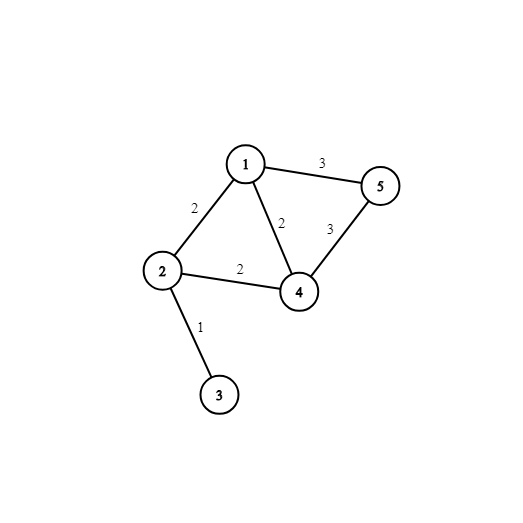
Вы можете, например, увеличить веса ребер $$$(1, 5)$$$ и $$$(2, 4)$$$ на $$$1$$$ для унификации MST.
| Название |
|---|




