| Codeforces Round 530 (Div. 2) |
|---|
| Закончено |
Mitya and Vasya are playing an interesting game. They have a rooted tree with $$$n$$$ vertices, and the vertices are indexed from $$$1$$$ to $$$n$$$. The root has index $$$1$$$. Every other vertex $$$i \ge 2$$$ has its parent $$$p_i$$$, and vertex $$$i$$$ is called a child of vertex $$$p_i$$$.
There are some cookies in every vertex of the tree: there are $$$x_i$$$ cookies in vertex $$$i$$$. It takes exactly $$$t_i$$$ time for Mitya to eat one cookie in vertex $$$i$$$. There is also a chip, which is initially located in the root of the tree, and it takes $$$l_i$$$ time to move the chip along the edge connecting vertex $$$i$$$ with its parent.
Mitya and Vasya take turns playing, Mitya goes first.
- Mitya moves the chip from the vertex, where the chip is located, to one of its children.
- Vasya can remove an edge from the vertex, where the chip is located, to one of its children. Vasya can also decide to skip his turn.
Mitya can stop the game at any his turn. Once he stops the game, he moves the chip up to the root, eating some cookies along his way. Mitya can decide how many cookies he would like to eat in every vertex on his way. The total time spent on descend, ascend and eating cookies should not exceed $$$T$$$. Please note that in the end of the game the chip is always located in the root of the tree: Mitya can not leave the chip in any other vertex, even if he has already eaten enough cookies — he must move the chip back to the root (and every move from vertex $$$v$$$ to its parent takes $$$l_v$$$ time).
Find out what is the maximum number of cookies Mitya can eat, regardless of Vasya's actions.
The first line contains two integers $$$n$$$ and $$$T$$$ — the number of vertices in the tree and the time he has to accomplish his task ($$$2\le n \le 10^5$$$; $$$1\le T\le10^{18}$$$).
The second line contains $$$n$$$ integers $$$x_1$$$, $$$x_2$$$, ..., $$$x_n$$$ — number of cookies located in the corresponding vertex ($$$1\le x_i\le10^6$$$). The third line contains $$$n$$$ integers $$$t_1$$$, $$$t_2$$$, ..., $$$t_n$$$ — how much time it takes Mitya to eat one cookie in vertex $$$i$$$ ($$$1\le t_i\le10^6$$$).
Each of the following $$$n - 1$$$ lines describe the tree. For every $$$i$$$ from $$$2$$$ to $$$n$$$, the corresponding line contains two integers $$$p_i$$$ and $$$l_i$$$, where $$$p_i$$$ denotes the parent of vertex $$$i$$$ and $$$l_i$$$ denotes the time it takes Mitya to move the chip along the edge from vertex $$$i$$$ to its parent ($$$1\le p_i < i$$$, $$$0\le l_i \le 10^9$$$).
Output a single integer — maximum number of cookies Mitya can eat.
5 26 1 5 1 7 7 1 3 2 2 2 1 1 1 1 2 0 2 0
11
3 179 2 2 1 6 6 6 1 3 2 3
4
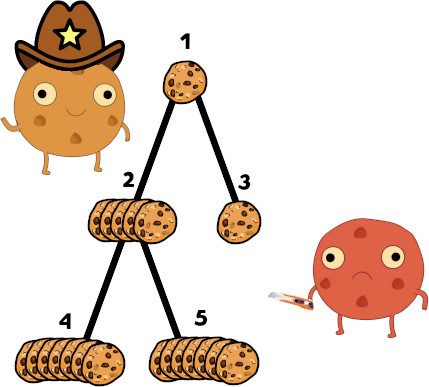
In the first example test case, Mitya can start by moving the chip to vertex $$$2$$$. In this case no matter how Vasya plays, Mitya is able to eat at least $$$11$$$ cookies. Below you can find the detailed description of the moves:
- Mitya moves chip to vertex $$$2$$$.
- Vasya removes edge to vertex $$$4$$$.
- Mitya moves chip to vertex $$$5$$$.
- Since vertex $$$5$$$ has no children, Vasya does not remove any edges.
- Mitya stops the game and moves the chip towards the root, eating cookies along the way ($$$7$$$ in vertex $$$5$$$, $$$3$$$ in vertex $$$2$$$, $$$1$$$ in vertex $$$1$$$).
Mitya spend $$$1+0$$$ time to go down, $$$0+1$$$ to go up, $$$7\cdot 2$$$ to eat $$$7$$$ cookies in vertex 5, $$$3\cdot 3$$$ to eat $$$3$$$ cookies in vertex 2, $$$1\cdot 1$$$ to eat $$$1$$$ cookie in vertex 1. Total time is $$$1+0+0+1+7\cdot 2+3\cdot 3+1\cdot 1=26$$$.
| Название |
|---|




