| Hello 2019 |
|---|
| Закончено |
Алексей решил попытать счастья в телешоу. Однажды он сходил на викторину. После того, как он идеально ответил на вопросы «Как обычно называют псевдоним в интернете?» («Ум... может быть ник?»), «В честь какого известного изобретателя назвали единицу силы магнитного поля?» («Ум... Никола Тесла?»), он решил посетить гораздо более сложное телешоу: «Что в этом мультимножестве?!».
Это телешоу устроено следующим образом: есть $$$n$$$ мультимножеств, пронумерованных от $$$1$$$ до $$$n$$$. Каждое из них изначально пусто. Затем, происходят $$$q$$$ запросов, где каждый запрос имеет один из четырёх следующих типов:
- 1 x v — присвоить $$$x$$$-му мультимножеству мультимножество из одного элемента $$$\{v\}$$$.
- 2 x y z — присвоить $$$x$$$-му мультимножеству объединение мультимножеств $$$y$$$ и $$$z$$$. For example: $$$\{1, 3\}\cup\{1, 4, 4\}=\{1, 1, 3, 4, 4\}$$$.
- 3 x y z — присвоить $$$x$$$-му мультимножеству произведение $$$y$$$-го и $$$z$$$-го мультимножества. Произведение $$$A \times B$$$ мультимножеств $$$A$$$ и $$$B$$$ определяется как $$$\{ \gcd(a, b)\, \mid\, a \in A,\, b \in B \}$$$, где $$$\gcd(p, q)$$$ обозначает наибольший общий делитель $$$p$$$ и $$$q$$$. Например, $$$\{2, 2, 3\} \times \{1, 4, 6\}=\{1, 2, 2, 1, 2, 2, 1, 1, 3\}$$$.
- 4 x v — вас спрашивают, сколько раз число $$$v$$$ встречается в мультимножестве $$$x$$$. Так как викторина показал себя достаточно сложной в прошлом, то теперь нужно лишь сказать ответ на этот вопрос по модулю $$$2$$$.
Обратите внимание, что $$$x$$$, $$$y$$$, и $$$z$$$ в описании выше не обязательно различны. Для запросов $$$2$$$-го и $$$3$$$-го типа нужно сначала вычислить соответствующую сумму или произведение и лишь затем выполнить присвоение.
Алексея смущают запутанные правила шоу. Помогите ему узнать ответы на все запросы $$$4$$$-го типа.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$1 \leq n \leq 10^5$$$, $$$1 \leq q \leq 10^6$$$) — количество мультимножеств и количество запросов.
Каждая из следующих $$$q$$$ строк содержит описание очередного запроса в формате, данном в условии. Гарантируется, что $$$1 \leq x,y,z \leq n$$$ и $$$1 \leq v \leq 7000$$$
Гарантируется, что есть хотя бы один запрос $$$4$$$-го типа.
Выведите строку из $$$0$$$ и $$$1$$$, имеющую длину равную количеству запросов $$$4$$$-го типа, $$$i$$$-й символ строки должен быть равен ответу на $$$i$$$-й запрос $$$4$$$-го типа.
4 13 1 1 1 1 2 4 1 3 6 4 4 4 1 4 4 2 2 1 2 2 3 3 4 4 4 4 3 2 2 3 4 2 1 4 2 2 4 2 3 4 2 4
010101
Мультимножества в тесте из примера выглядят следующим образом ($$$i$$$ обозначает количество уже обработанных запросов).
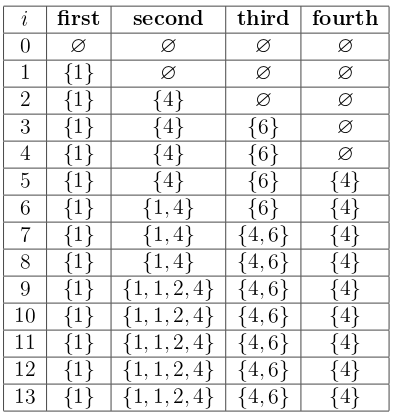
| Название |
|---|




