| Good Bye 2018 |
|---|
| Закончено |
Боб — пират, ищущий величайшее сокровище, которое когда-либо видел мир. Известно, что сокровище расположено в точке $$$T$$$, координаты которой только предстоит узнать.
Боб путешествовал по миру и собирал подсказки о сокровище в $$$n$$$ обелисках. Эти подсказки были на древнем языке, и он смог их расшифровать только дома. Поскольку он не знает, какая подсказка принадлежит какому обелиску, поиск сокровища может стать проблемой. Вы можете помочь ему?
Как известно, мир — это двумерная плоскость. $$$i$$$-й обелиск находится в целочисленных координатах $$$(x_i, y_i)$$$. $$$j$$$-я подсказка состоит из $$$2$$$ целых чисел $$$(a_j, b_j)$$$ и принадлежит обелиску $$$p_j$$$, где $$$p$$$ — некоторая (неизвестная) перестановка из $$$n$$$ элементов. Это означает, что сокровище находится в точке $$$T=(x_{p_j} + a_j, y_{p_j} + b_j)$$$. Эта точка $$$T$$$ должно быть одинакова для всех подсказок.
Другими словами, каждая подсказка принадлежит ровно одному из обелисков, и у каждого обелиска есть ровно одна принадлежащая ему подсказка. Подсказка представляет вектор от обелиска к сокровищу. Подсказки должны быть распределены среди обелисков таким образом, чтобы все они указывали на одну и ту же позицию сокровища.
Ваша задача — найти координаты клада. Если существует несколько решений, вы можете вывести любое из них.
Обратите внимание, что вам не нужно находить перестановку. Перестановки используются только для объяснения задачи.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 1000$$$) — количество обелисков, оно же равно количество подсказок.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$, $$$y_i$$$ ($$$-10^6 \leq x_i, y_i \leq 10^6$$$) — координаты $$$i$$$-го обелиска. Все координаты различны, то есть $$$x_i \neq x_j$$$ или $$$y_i \neq y_j$$$ выполняется для каждой пары $$$(i, j)$$$, такой что $$$i \neq j$$$.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$a_i$$$, $$$b_i$$$ ($$$-2 \cdot 10^6 \leq a_i, b_i \leq 2 \cdot 10^6$$$) — направление $$$i$$$-й подсказки. Все координаты различны, то есть $$$a_i \neq a_j$$$ или $$$b_i \neq b_j$$$ выполняется для каждой пары $$$(i, j)$$$, такой что $$$i \neq j$$$.
Гарантируется, что существует перестановка $$$p$$$ такая, что для каждой пары $$$i,j$$$ правда, что $$$\left(x_{p_i} + a_i, y_{p_i} + b_i\right) = \left(x_{p_j} + a_j, y_{p_j} + b_j\right)$$$.
Выведите два числа $$$T_x, T_y$$$ — координаты сокровища.
Если существует несколько решений, выведите любое из них.
2 2 5 -6 4 7 -2 -1 -3
1 2
4 2 2 8 2 -7 0 -2 6 1 -14 16 -12 11 -18 7 -14
9 -12
Поскольку $$$n = 2$$$, мы можем рассмотреть все перестановки двух элементов.
Если $$$p = [1, 2]$$$, то обелиск $$$(2, 5)$$$ содержит подсказку $$$(7, -2)$$$, которая значит, что сокровище спрятано в $$$(9, 3)$$$. Второй обелиск $$$(-6, 4)$$$ содержал бы подсказку $$$(-1,-3)$$$ и сокровище было бы в $$$(-7, 1)$$$. Однако оба обелиска должны указывать одно и то же местоположение, поэтому это явно неправильная перестановка.
Если же спрятанная перестановка — это $$$[2, 1]$$$, тогда первая подсказка принадлежит второму обелиску, а вторая подсказка первому обелиску. Поэтому $$$(-6, 4) + (7, -2) = (2,5) + (-1,-3) = (1, 2)$$$, значит $$$T = (1,2)$$$ — это местоположение сокровища.
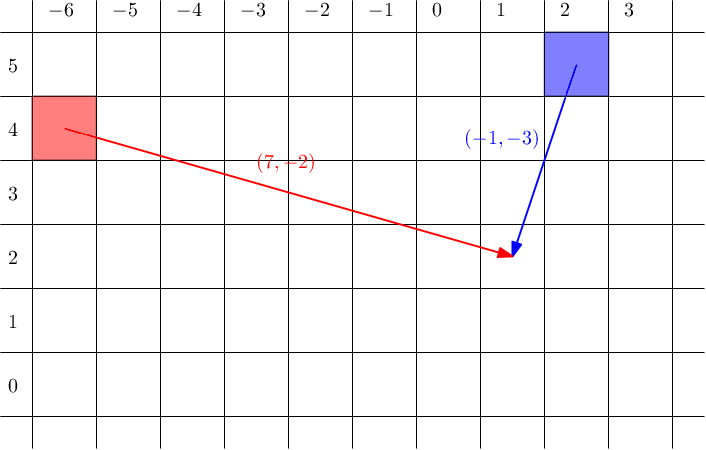
Во втором примере скрытая перестановка — $$$[2, 3, 4, 1]$$$.
| Название |
|---|




