| Технокубок 2019 - Отборочный Раунд 4 |
|---|
| Закончено |
Национальный лес Квадрляндии был разделен на одинаковые квадратные участки размером $$$1 \times 1$$$, выровненные по направлениям с севера на юг и с востока на запад. Каждый участок может быть однозначно задан целочисленными Декартовыми координатами $$$(x, y)$$$ своего юго-западного угла.
Три друга, Алиса, Боб и Чарли собираются купить три отдельных участка земли $$$A, B, C$$$ в лесу. Изначально все участки в лесу (включая участки $$$A, B, C$$$) покрыты деревьями. Друзья хотят навещать друг друга, поэтому они хотят очистить некоторые участки от деревьев. После очистки, можно будет добраться до любого из участков $$$A, B, C$$$ от любого другого, перемещаясь по соседним очищенным участкам. Два земельных участка являются соседними, если они имеют общую сторону.
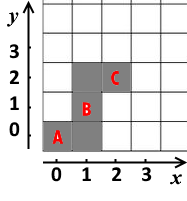 Например, $$$A=(0,0)$$$, $$$B=(1,1)$$$, $$$C=(2,2)$$$. Необходимо очистить как минимум $$$5$$$ участков, чтобы соединить друзей. Эти участки выделены серым цветом.
Например, $$$A=(0,0)$$$, $$$B=(1,1)$$$, $$$C=(2,2)$$$. Необходимо очистить как минимум $$$5$$$ участков, чтобы соединить друзей. Эти участки выделены серым цветом. Конечно, друзья не хотят слишком напрягаться. Помогите им найти наименьшее количество участков, которые они должны очистить от деревьев.
Первая строка содержит два целых числа $$$x_A$$$ и $$$y_A$$$ — координаты участка $$$A$$$ ($$$0 \leq x_A, y_A \leq 1000$$$). Следующие две строки описывают координаты $$$(x_B, y_B)$$$ и $$$(x_C, y_C)$$$ участков $$$B$$$ и $$$C$$$, соответственно, в таком же формате ($$$0 \leq x_B, y_B, x_C, y_C \leq 1000$$$). Гарантируется, что все три участка различны.
В первой строке выведите одно целое число $$$k$$$ — наименьшее количество участков, которые необходимо очистить от деревьев. Следующие $$$k$$$ строк должны содержать координаты всех участков, которые необходимо очистить. Все $$$k$$$ участков должны быть различны. Участки можно вывести в любом порядке.
Если решений несколько, выведите любое из них.
0 0 1 1 2 2
5 0 0 1 0 1 1 1 2 2 2
0 0 2 0 1 1
4 0 0 1 0 1 1 2 0
Первый пример показан на картинке в условии задачи.
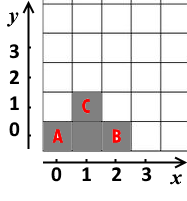
Второй пример изображен на этой картинке:
| Название |
|---|




