Ура, конструктивные графовые задачи вернулись! В этот раз надо построить граф со следующими свойствами.
Граф называется связным тогда и только тогда, когда существует путь между любой парой вершин.
Диаметр (также «длиннейший кратчайший путь») связного неориентированного графа — это максимальное число ребер на кратчайшем пути между всеми парами вершин.
Степень вершины равна количеству инцидентных ей ребер.
По заданной последовательности из $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ постройте связный неориентированный граф, состоящий из $$$n$$$ вершин, такой, чтобы:
- в графе не содержалось петель и кратных ребер;
- степень $$$d_i$$$ вершины $$$i$$$ не превышала $$$a_i$$$ (то есть $$$d_i \le a_i$$$);
- диаметр графа максимально возможный.
Выведите полученный граф или сообщите, что ответа не существует.
В первой строке записано одно целое число $$$n$$$ ($$$3 \le n \le 500$$$) — количество вершин в графе.
Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le n - 1$$$) — ограничения на степени вершин.
Выведите «NO», если невозможно построить граф с заданными ограничениями.
В противном случае выведите «YES» и диаметр полученного графа в первой строке.
Во второй строке выведите единственное целое число $$$m$$$ — количество ребер в полученном графе.
В $$$i$$$-й из следующих $$$m$$$ строк выведите два целых числа $$$v_i, u_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$v_i \neq u_i$$$) — описание $$$i$$$-го ребра. Граф не должен содержать кратных ребер — для каждой выведенной пары $$$(x, y)$$$ вывод не должен содержать больше пар $$$(x, y)$$$ и $$$(y, x)$$$.
3 2 2 2
YES 2 2 1 2 2 3
5 1 4 1 1 1
YES 2 4 1 2 3 2 4 2 5 2
3 1 1 1
NO
На картинках изображены графы для первых двух примеров. Оба графа имеют диаметр $$$2$$$.
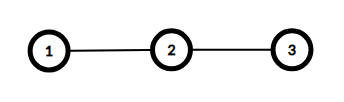$$$d_1 = 1 \le a_1 = 2$$$$$$d_2 = 2 \le a_2 = 2$$$
$$$d_3 = 1 \le a_3 = 2$$$
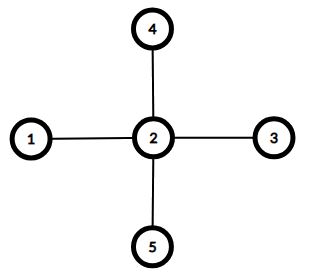$$$d_1 = 1 \le a_1 = 1$$$$$$d_2 = 4 \le a_2 = 4$$$
$$$d_3 = 1 \le a_3 = 1$$$
$$$d_4 = 1 \le a_4 = 1$$$
