На шахматной доске шириной $$$n$$$ и высотой $$$n$$$ строки нумеруются снизу вверх от $$$1$$$ до $$$n$$$, а столбцы нумеруются слева направо от $$$1$$$ до $$$n$$$. Поэтому, каждой клетке шахматной доски можно присвоить координаты $$$(r,c)$$$, где $$$r$$$ — номер строки, а $$$c$$$ — номер столбца.
В клетке с координатами $$$(1,1)$$$ уже тысячу лет сидит белый король, а в клетке с координатами $$$(n,n)$$$ сидит чёрный король. Они бы сидели так и дальше, но тут в клетку с координатами $$$(x,y)$$$ упала красивая монетка...
Каждый из монархов захотел её получить, так что они решили устроить забег по немного изменённым шахматным правилам:
Как и в шахматах, первый ход делает белый король, второй — чёрный, третий — белый и так далее. Однако в этой задаче короли могут находиться в соседних или даже в одной клетке одновременно.
Кто первым добежит до монетки, тот и победит. То есть победит тот, кто первым окажется в клетке с координатами $$$(x,y)$$$.
Напомним, что король — это такая шахматная фигура, которая может двигаться на одну клетку во все стороны, то есть, если король стоит в клетке $$$(a,b)$$$, то за один ход он может перейти из $$$(a,b)$$$ в клетки $$$(a + 1,b)$$$, $$$(a - 1,b)$$$, $$$(a,b + 1)$$$, $$$(a,b - 1)$$$, $$$(a + 1,b - 1)$$$, $$$(a + 1,b + 1)$$$, $$$(a - 1,b - 1)$$$, $$$(a - 1,b + 1)$$$. Выходить за пределы поля запрещено.
Определите цвет короля, который первым окажется в клетке с координатами $$$(x,y)$$$, если первым ходит белый король.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 10^{18}$$$) — длина стороны шахматного поля.
Вторая строка содержит два целых числа $$$x$$$ и $$$y$$$ ($$$1 \le x,y \le n$$$) — координаты клетки, в которую упала монетка.
В единственной строке выведите «White» (без кавычек), если победит белый король, или «Black» (без кавычек), если победит чёрный король.
Вы можете выводить каждую букву в любом регистре (строчную или заглавную).
4
2 3
White
5
3 5
Black
2
2 2
Black
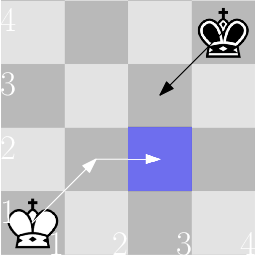
Пример гонки в первом примере, где белый и чёрный короли действуют оптимально:
- Белый король переходит из клетки $$$(1,1)$$$ в $$$(2,2)$$$.
- Чёрный король переходит из клетки $$$(4,4)$$$ в $$$(3,3)$$$.
- Белый король переходит из клетки $$$(2,2)$$$ в $$$(2,3)$$$. Именно в эту клетку упала монетка, значит, белый король выиграл.
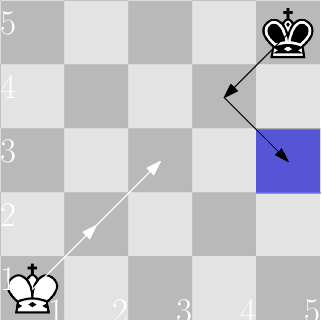
Пример гонки во втором примере, где белый и чёрный короли действуют оптимально:
- Белый король переходит из клетки $$$(1,1)$$$ в клетку $$$(2,2)$$$.
- Чёрный король переходит из клетки $$$(5,5)$$$ в клетку $$$(4,4)$$$.
- Белый король переходит из клетки $$$(2,2)$$$ в клетку $$$(3,3)$$$.
- Чёрный король переходит из клетки $$$(4,4)$$$ в $$$(3,5)$$$. В этой клетке лежит монетка, значит, чёрный король выиграл.
Объяснение к третьему примеру. Так как чёрный король изначально стоит в клетке, куда упала монетка, то он выиграл.

| Название |
|---|