Ваня — начинающий художник. У него есть $$$n$$$ красок разных цветов. Он знает ровно $$$m$$$ пар цветов, которые сочетаются между собой.
Также Ваня любит играть в шахматы. У Вани есть $$$5000$$$ ладей. Он хочет взять $$$k$$$ ладей, раскрасить каждую из них в один из $$$n$$$ цветов, а затем расставить эти $$$k$$$ ладей на шахматной доске размера $$$10^{9} \times 10^{9}$$$.
Будем называть множество ладей на доске связным, если от любой ладьи можно добраться до любой другой из этого множества, делая ходы только на те клетки, где стоят ладьи этого множества. Считайте, что ладья может перепрыгивать через другие ладьи, то есть ладья может ходить в любую клетку на одной вертикали с ней, и в любую клетку на одной горизонтали с ней.
Ваня хочет, чтобы для его расстановки выполнялись следующие свойства:
- Для каждого цвета на доске есть хотя бы одна ладья этого цвета;
- Для каждого цвета множество ладей этого цвета связно;
- Для любых двух разных цветов $$$a$$$ $$$b$$$ объединение множества ладей цвета $$$a$$$ и множества ладей цвета $$$b$$$ связно в том и только в том случае, если эти два цвета сочетаются между собой.
Помогите Ване найти такую расстановку ладей на доске.
В первой строке записаны $$$2$$$ целых числа $$$n$$$, $$$m$$$ ($$$1 \le n \le 100$$$, $$$0 \le m \le min(1000, \,\, \frac{n(n-1)}{2})$$$) — количество цветов и количество пар сочетающихся цветов.
В следующих $$$m$$$ строках заданы пары сочетающихся цветов. Цвета пронумерованы от $$$1$$$ до $$$n$$$. Гарантируется, что каждая пара встречается в списке не более одного раза.
Выведите $$$n$$$ блоков, $$$i$$$-й блок описывает ладьи $$$i$$$-го цвета.
В первой строке описания выведите одно число $$$a_{i}$$$ ($$$1 \le a_{i} \le 5000$$$) — количество ладей цвета $$$i$$$. В последующих $$$a_{i}$$$ строках выведите по два числа $$$x$$$ и $$$y$$$ ($$$1 \le x, \,\, y \le 10^{9}$$$) — координаты очередной ладьи.
Все выведенные ладьи должны стоять на разных клетках.
Общее количество ладей не должно превышать $$$5000$$$.
Гарантируется, что при заданных ограничениях решение всегда существует.
3 2
1 2
2 3
2
3 4
1 4
4
1 2
2 2
2 4
5 4
1
5 1
3 3
1 2
2 3
3 1
1
1 1
1
1 2
1
1 3
3 1
1 3
1
1 1
1
2 2
1
3 1
Расстановки ладей для всех трех примеров (красный — это цвет $$$1$$$, зелёный — цвет $$$2$$$, синий — цвет $$$3$$$).
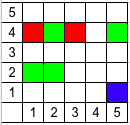
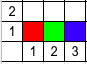
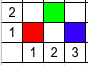
| Название |
|---|




