Ваня расставляет коней на бесконечной шахматной доске. Изначально на доске стоят $$$n$$$ коней. Если пустую клетку бьют хотя бы $$$4$$$ уже поставленных коня, то на неё ставится новый конь. Ваня повторяет эту операцию, пока есть такая пустая клетка. Несложно показать, что процесс конечен. Также несложно показать, что конечная расстановка коней на доске не зависит от порядка, в котором на доску выставляются новые кони.
Ваня попросил вас найти начальную расстановку из $$$n$$$ коней на доске такую, чтобы в конце процесса на доске оказалось не менее $$$\lfloor \frac{n^{2}}{10} \rfloor$$$ коней.
Первая и единственная строка содержит одно число $$$n$$$ ($$$1 \le n \le 10^{3}$$$) — количество коней в изначальной расстановке.
Выведите $$$n$$$ строк, в каждой строке выведите $$$2$$$ числа $$$x_{i}$$$ и $$$y_{i}$$$ ($$$-10^{9} \le x_{i}, \,\, y_{i} \le 10^{9}$$$) — координаты $$$i$$$-го коня. Для всех $$$i \ne j$$$ должно быть верно, что $$$(x_{i}, \,\, y_{i}) \ne (x_{j}, \,\, y_{j})$$$. То есть все кони должны стоять на различных клетках.
Гарантируется, что решение существует.
4
1 1
3 1
1 5
4 4
7
2 1
1 2
4 1
5 2
2 6
5 7
6 6
Посмотрим на второй пример:
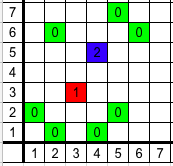
Зелёные нули — это изначальные кони. Клетка $$$(3, \,\, 3)$$$ находится под ударом $$$4$$$ коней на клетках $$$(1, \,\, 2)$$$, $$$(2, \,\, 1)$$$, $$$(4, \,\, 1)$$$ и $$$(5, \,\, 2)$$$, поэтому Ваня поставит нового коня в эту клетку. Клетка $$$(4, \,\, 5)$$$ изначально находится под атакой лишь $$$3$$$ коней на клетках $$$(2, \,\, 6)$$$, $$$(5, \,\, 7)$$$ и $$$(6, \,\, 6)$$$. Однако новый конь в клетке $$$(3, \,\, 3)$$$ тоже атакует клетку $$$(4, \,\, 5)$$$, теперь эта клетка находится под атакой $$$4$$$ коней, и Ваня поставит нового коня в эту клетку. Больше не осталось свободных клеток, которые находятся под атакой $$$4$$$ или более коней, поэтому процесс останавливается. В конце процесса на доске оказалось $$$9$$$ коней, что не меньше $$$\lfloor \frac{7^{2}}{10} \rfloor = 4$$$.
| Название |
|---|




