| Mail.Ru Cup 2018 Раунд 2 |
|---|
| Закончено |
За последнее время Боб заметно растолстел. Чтобы похудеть, Боб решил заняться плаванием в бассейне, но перед тем как он пошёл в бассейн первый раз, ему приснился очень странный сон. Во сне Боб плыл по одной из дорожек бассейна, а в этом бассейне помимо Боба плавали медузы. Стоит ли говорить, что медузы всегда были одним из самых глубоких детских страхов Боба.
Для простоты, примем следующую физическую модель:
- Дорожка бассейна представляет собой часть плоскости, ограниченную прямыми $$$x=0$$$ и $$$x=w$$$. Боб не имеет права выплывать с дорожки, но может касаться её границы.
- Сами медузы очень маленькие, но во сне Боба они очень шустрые. У каждой медузы есть своя область активности в форме круга вокруг неё. У двух разных медуз зоны могут перекрываться или даже быть вложенными.
- Боб имеет форму выпуклого многоугольника.
- К сожалению, лишний вес сделал его совершенно неповоротливым, то есть плавание Боба представляет собой параллельный перенос. Но при этом в каждый конкретный момент времени направление этого переноса может быть любым.
- Если Боб заплывает в область активности медузы, она его замечает, догоняет и очень больно ужаливает. Считается, что Боб заплыл в область активности медузы, если в какой-то момент времени пересечение его многоугольника с этой областью имеет ненулевую площадь (в частности, если они только касаются, медуза не заметит Боба).
- Если медуза ужалила Боба, она довольная уплывает по своим делам и больше опасности не представляет.
Бобу нужно проплыть всю дорожку бассейна и быть ужаленным минимальное число раз. Он начинает движение на прямой $$$y=-h$$$, а закончить должен на прямой $$$y=h$$$, где $$$h = 10^{10}$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$w$$$ ($$$3 \le n \le 200, 1 \le w \le 30000$$$) — количество вершин в многоугольнике, описывающем форму Боба, и ширина дорожки.
Следующие $$$n$$$ строк содержат по два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$0 \le x_i \le w, 0 \le y_i \le 30000$$$) — координаты вершин многоугольника в обходе против часовой стрелки. Гарантируется, что данный многоугольник является строго выпуклым.
Следующая строка содержит одно целое число $$$m$$$ ($$$0 \le m \le 200$$$) — количество медуз в бассейне.
Наконец, следующие $$$m$$$ строк содержат по три целых числа $$$x_i$$$, $$$y_i$$$, $$$r_i$$$ ($$$0 \le x_i \le w, 0 \le y_i \le 30000, 1 \le r_i \le 30000$$$) — координаты $$$i$$$-й медузы и радиус её области активности. Гарантируется, что никакие две медузы не находятся в одной точке.
Выведите одно число — минимальное число медуз, которые ужалят Боба, если он будет действовать оптимальным образом.
4 4
0 0
2 0
2 2
0 2
3
1 1 1
3 5 1
1 9 1
0
4 6
0 0
3 0
3 3
0 3
3
1 0 1
4 2 2
3 6 1
2
4 2
0 0
1 0
1 1
0 1
2
1 1 1
1 3 1
2
Ниже вы можете увидеть визуализацию возможных решение первого и второго примера:
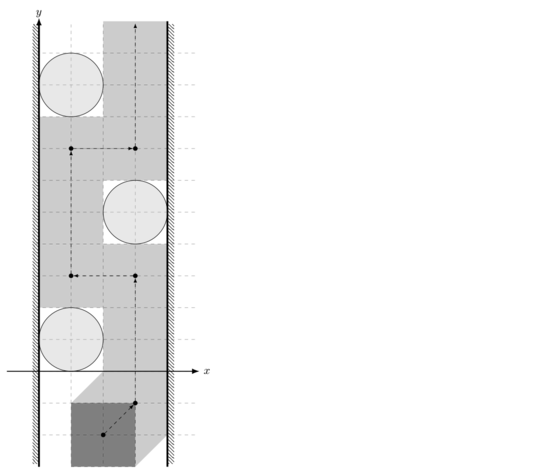

| Название |
|---|




