| Mail.Ru Cup 2018 Раунд 1 |
|---|
| Закончено |
Король некоторой страны $$$N$$$ решил полностью перестроить дорожную систему. В стране проживает $$$n$$$ человек, пронумерованных от $$$1$$$ до $$$n$$$. Можно проводить двустороннюю дорогу от домика жителя этой страны с номером $$$a$$$ к домику другого жителя этой страны с номером $$$b$$$. Между каждой парой жителей не может быть построено больше одной дороги. Конечно система дорог должна быть связной, то есть от любого домика можно дойти до другого передвигаясь по дорогам. Для экономии средств было решено построить $$$n-1$$$ дорогу, то есть, система дорог должна образовывать дерево.
Но не все так просто, ведь не зря король обратился именно к вам за помощью. В стране есть $$$m$$$ тайных обществ, известных только королю, каждое из которых является непустым подмножеством её жителей. Поскольку он не хочет вступать в конфликт ни с одним из этих обществ, он хочет построить дорожную систему, которая будет удовлетворять следующему условию: все домики жителей каждого тайного общества должны образовывать связное поддерево. Будем считать, что некоторое подмножество вершин дерева образует связное поддерево тогда и только тогда, когда выполнено условие: если оставить только вершины этого подмножества и ребра дерева, соединяющие только вершины из подмножества, то полученный граф будет связным.
Помогите королю определить, возможно ли построить такую дорожную систему или нет, и если возможно, постройте её.
Каждый тест содержит один или несколько тестовых случаев.
На первой строке входного файла находится единственное число $$$t$$$ ($$$1 \leq t \leq 2000$$$) — количество тестовых случаев.
В следующих строках следуют описания этих тестовых случаев в следующем формате.
На первой строке находятся два целых числа $$$n$$$ и $$$m$$$ ($$$1 \leq n, m \leq 2000$$$) — количество жителей в стране и количество тайных обществ.
В следующих $$$m$$$ строках находится описание тайных обществ. В $$$i$$$-й из этих строк находится строка $$$s_i$$$ длины $$$n$$$, состоящая из символов «0» и «1». Житель с номером $$$j$$$ принадлежит $$$i$$$-му тайному обществу тогда и только тогда, когда $$$s_{{i}{j}}=1$$$. Гарантируется, что в строке $$$s_i$$$ есть хотя бы один символ «1» для любого $$$1 \leq i \leq m$$$.
Гарантируется, что сумма всех $$$n$$$ для всех тестовых случаев не превосходит $$$2000$$$ и сумма всех $$$m$$$ для всех тестовых случаев не превосходит $$$2000$$$.
Выведите ответы для всех тестовых случаев в том порядке, в котором они заданы во входных данных, в следующем формате.
Если дорожную систему построить невозможно, в единственной строке выведите «NO» (без кавычек).
В противном случае в первой строке выведите «YES» (без кавычек).
В следующих $$$n-1$$$ строках выведите описание дорожной системы: в каждой строке должно находиться по два целых числа $$$a$$$, $$$b$$$, которые будут означать, что нужно провести дорогу между домиками жителей $$$a$$$ и $$$b$$$ ($$$1 \leq a, b \leq n$$$, $$$a \neq b$$$).
Проведенные дороги должны образовывать дерево, и домики каждого общества должны образовывать связное поддерево.
2
4 3
0011
1110
0111
3 3
011
101
110
YES
1 3
2 3
3 4
NO
В первом тестовом случае можно построить такую дорожную систему:
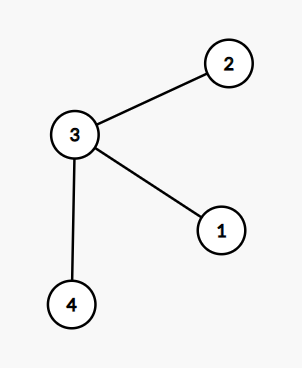
Легко убедиться, что для каждого тайного общества все домики его жителей образуют связное поддерево. Например, во $$$2$$$-м тайном обществе состоят жители с номерами $$$1$$$, $$$2$$$, $$$3$$$. Они образуют связное поддерево, так как если оставить только домики $$$1$$$, $$$2$$$, $$$3$$$ и дороги между ними, то останутся две дороги: между $$$1$$$ и $$$3$$$ и между $$$2$$$ и $$$3$$$, то есть связный граф.
Во втором тестовом случае можно убедиться, что не существует ни одной дорожной системы, подходящей королю.
| Название |
|---|




