| Mail.Ru Cup 2018 Раунд 1 |
|---|
| Закончено |
Паша — начинающий техник, но уже поставил себе большую цель собрать собственный компьютер. Первая непростая задача — научиться собирать электрическую схему.
Схема, которую собрал Паша, состоит из несколько проводов. Каждый провод — это отрезок, который соединяет две точки на плоскости с целыми координатами, лежащими в диапазоне $$$[1, 10^9]$$$.
В схеме есть провода двух цветов:
- красные провода: эти провода должны иметь вид горизонтального отрезка, то есть если провод соединяет две точки $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$, то выполнено, что $$$y_1 = y_2$$$;
- синие провода: эти провода должны иметь вид вертикального отрезка, то есть если провод соединяет две точки $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$, то выполнено, что $$$x_1 = x_2$$$.
Обратите внимание, что если провод соединяет две одинаковые точки, то он может быть как красным, так и синим. Также в Пашиной схеме никакие два провода одного цвета не могут пересекаться, то есть любые два отрезка проводов одного цвета не могут содержать общих точек.
Недоработка Пашиной схемы состоит в том, что его провода не были изолированы, и поэтому в точках пересечения проводов разных цветов возникли искры, которые Паша увидел. Он записал все точки, в которых он увидел искру. У него получилось множество из $$$n$$$ различных точек. После чего он разобрал схему и пошёл спать.
Утром, когда Паша увидел на листочке множество из $$$n$$$ точек, в которых он увидел искру, ему стало интересно, сколько проводов он использовал, собрав эту схему. К сожалению, он ничего не запомнил, поэтому он решил узнать, какое минимальное количество проводов он мог использовать в своей схеме. Помогите ему узнать это число, а также расположить эти провода так, чтобы в получившейся схеме искры возникли в тех же самых точках.
В первой строке находится одно целое число $$$n$$$ ($$$1 \leq n \leq 1000$$$) — количество точек, в которых Паша увидел искру.
В следующих $$$n$$$ строках находится по два целых числа $$$x$$$ и $$$y$$$ ($$$1 \leq x, y \leq 10^9$$$) — координаты очередной точки. Гарантируется, что все точки различны.
Выведите описание электрической схемы в следующем формате:
Сначала выведите $$$h$$$ — количество горизонтальных красных проводов ($$$0 \leq h$$$). В следующих $$$h$$$ строках выведите по $$$4$$$ целых числа $$$x_1$$$, $$$y_1$$$, $$$x_2$$$, $$$y_2$$$ — координаты двух точек $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$, которые соединяет очередной красный провод. Поскольку отрезки горизонтальные, должно быть выполнено $$$y_1 = y_2$$$. Также должно быть выполнено $$$1 \leq x_1, y_1, x_2, y_2 \leq 10^9$$$.
Потом выведите $$$v$$$ — количество вертикальных синих проводов ($$$0 \leq v$$$). В следующих $$$v$$$ строках выведите по $$$4$$$ целых числа $$$x_1$$$, $$$y_1$$$, $$$x_2$$$, $$$y_2$$$ — координаты двух точек $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$, которые соединяет синий очередной провод. Поскольку отрезки вертикальные, должно быть выполнено $$$x_1 = x_2$$$. Также должно быть выполнено $$$1 \leq x_1, y_1, x_2, y_2 \leq 10^9$$$.
Никакие два отрезка одного цвета не должны иметь общих точек. Множество точек, в которых Паша мог увидеть искру, если бы он построил такую схему, должно совпадать с данным во входных данных множеством точек.
Количество отрезков $$$(h + v)$$$ должно быть минимально возможным. Можно легко показать, что ответ всегда существует. Если существует несколько возможных ответов, выведите любой.
4
2 2
2 4
4 2
4 4
2
5 2 1 2
1 4 5 4
2
2 1 2 5
4 5 4 1
4
2 1
3 2
2 3
1 2
4
2 1 2 1
3 2 3 2
1 2 1 2
2 3 2 3
3
1 2 1 2
3 2 3 2
2 3 2 1
В первом примере Паша мог собрать такую схему:
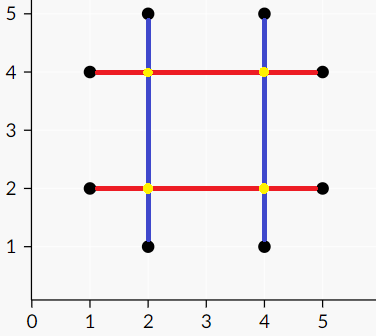
В этой схеме по $$$2$$$ провода каждого цвета: красные из $$$(5, 2)$$$ в $$$(1, 2)$$$ и из $$$(1, 4)$$$ в $$$(5, 4)$$$, синие из $$$(2, 1)$$$ в $$$(2, 5)$$$ и из $$$(4, 5)$$$ в $$$(4, 1)$$$. Заметим, что он увидит искры ровно в тех точках, которые он записал (обозначены желтым цветом на картинке). Например, искру в точке $$$(2, 4)$$$ он увидит, так как в этой точке пересекаются второй красный провод и первый синий. Можно доказать, что нужно не меньше $$$4$$$-х проводов, чтобы получить схему, нужную Паше.
| Название |
|---|




