Вы играете в странную игру с Ли Ченом. У вас есть дерево с $$$n$$$ вершинами, нарисованное на листе бумаги. Вершины дерева не пронумерованы, но различимы. Каждый из вас независимо пронумеровал вершины целыми числами от $$$1$$$ до $$$n$$$. Вы не знаете нумерацию друг друга.
Вы и Ли Чен выбрали по поддереву (то есть связному подграфу) в этом дереве. При этом ваше поддерево в вашей нумерации состоит из вершин $$$x_1, x_2, \ldots, x_{k_1}$$$, а поддерево Ли Чена в его нумерации состоит из вершин $$$y_1, y_2, \ldots, y_{k_2}$$$. Значения $$$x_1, x_2, \ldots, x_{k_1}$$$ и $$$y_1, y_2, \ldots, y_{k_2}$$$ известны вам обоим.
Вы хотите узнать, есть ли хотя бы одна общая вершина у ваших поддеревьев. К счастью, ваш друг Андрей знает ваши с Ли Ченом нумерации. Вы можете спросить у Андрея не более $$$5$$$ вопросов, каждый из которых один из следующих двух типов:
- A x: Андрей посмотрит на вершину $$$x$$$ в вашей нумерации и скажет вам ее номер в нумерации Ли Чена;
- B y: Андрей посмотрит на вершину $$$y$$$ в нумерации Ли Чена и скажет вам ее номер в вашей нумерации.
Выясните, есть ли общая вершина у ваших поддеревьев. Если есть, то найдите обозначение любой одной из этих вершин в вашей нумерации.
Каждый тест состоит из нескольких тестовых случаев.
Сначала считайте строку, которая содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 100$$$) — количество тестовых случаев.
Далее для каждого тестового случая ваша программа должна взаимодействовать с программой жюри следующим образом.
В первой строке считайте одно целое число $$$n$$$ ($$$1 \leq n \leq 1\,000$$$) — количество вершин в дереве.
Далее в каждой из следующих $$$n-1$$$ строк считайте два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1\leq a_i, b_i\leq n$$$) — ребро дерева, которое соединяет вершины $$$a_i$$$ и $$$b_i$$$, в соответствии с вашей нумерацией вершин.
В следующей строке считайте одно целое число $$$k_1$$$ ($$$1 \leq k_1 \leq n$$$) — количество вершин в вашем поддереве.
Следующая строка содержит $$$k_1$$$ различных целых чисел $$$x_1,x_2,\ldots,x_{k_1}$$$ ($$$1 \leq x_i \leq n$$$) — номера вершин в вашем поддереве, в соответствии с вашей нумерацией. Гарантируется, что эти вершины формируют поддерево.
Следующая строка содержит одно целое число $$$k_2$$$ ($$$1 \leq k_2 \leq n$$$) — количество вершин в поддереве Ли Чена.
Следующая строка содержит $$$k_2$$$ различных целых чисел $$$y_1, y_2, \ldots, y_{k_2}$$$ ($$$1 \leq y_i \leq n$$$) — номера (в соответствии с нумерацией Ли Чена) вершин поддерева Ли Чена. Гарантируется, что вершины формируют поддерево, если мы применим скрытую перестановку Ли Чена на дереве, чтобы перенумеровать вершины.
Тесты будут предоставляться друг за другом, поэтому вы должны завершить взаимодействие с предыдущим тестовым случаем (то есть, выведя номер общей вершины или $$$-1$$$, если такой вершины нет), чтобы начать получать следующий.
Далее вы можете задавать Андрею два разных типа вопросов.
- Вы можете вывести «A x» ($$$1 \leq x \leq n$$$). Это значит, что Андрей посмотрит на вершину $$$x$$$ в вашей нумерации и скажет вам, какой номер имеет эта вершина в нумерации Ли Чена.
- Вы можете вывести «B y» ($$$1 \leq y \leq n$$$). Это значит, что Андрей посмотрит на вершину $$$y$$$ в нумерации Ли Чена и скажет вам, какой номер имеет эта вершина в вашей нумерации.
Вы можете задать не более $$$5$$$ вопросов в одном тестовом случае.
Когда вы готовы отвечать, выведите «C s», где $$$s$$$ — либо номер в вашей нумерации любой из вершин, которая есть в обоих поддеревьях, либо $$$-1$$$, если таких нет. Вывод ответа не считается вопросом. Не забудьте сбросить буфер вывода, чтобы перейти к следующему тестовому случаю.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если программа жюри возвращает $$$-1$$$ вместо ответа на запрос, это значит, что вы задали больше вопросов, чем разрешено, или задали недопустимый вопрос. Ваша программа должна немедленно завершиться (например, вызовом функции exit(0)). Вы получите вердикт Wrong Answer; это значит, что вы задали слишком много вопросов, или то, что вы задали некорректный запрос. Если вы это проигнорируете, вы можете получить любой другой вердикт, так как вы будете продолжать считывать из закрытого потока.
Входные данные для взломов
Чтобы взломать, используйте следующий формат. Обратите внимание, что вы можете взламывать только с одним тестовым случаем.
Первая строка должна содержать одне целое число $$$t$$$ ($$$t=1$$$).
Вторая строка должна содержать одно целое число $$$n$$$ ($$$1 \leq n \leq 1\,000$$$).
Третья строка содержит $$$n$$$ целых чисел $$$p_1, p_2, \ldots, p_n$$$ ($$$1\leq p_i\leq n$$$) — скрытая перестановка от $$$1$$$ до $$$n$$$. Эта перестановка задает нумерацию, которую использует Ли Чен. То есть вершина, которая у вас имеет номер $$$i$$$, имеет номер $$$p_i$$$ в нумерации Ли Чена.
Каждая из следующих $$$n-1$$$ строк должна содержать два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1\leq a_i, b_i\leq n$$$). Эти ребра должны формировать дерево.
Следующая строка должна содержать одно целое число $$$k_1$$$ ($$$1 \leq k_1 \leq n$$$).
Следующая строка должна содержать $$$k_1$$$ различных целых чисел $$$x_1,x_2,\ldots,x_{k_1}$$$ ($$$1 \leq x_i \leq n$$$). Эти вершины должны формировать поддерево.
Следующая строка должна содержать одно целое число $$$k_2$$$ ($$$1 \leq k_2 \leq n$$$).
Следующая строка должна содержать $$$k_2$$$ различных целых чисел $$$y_1, y_2, \ldots, y_{k_2}$$$ ($$$1 \leq y_i \leq n$$$). Эти вершины должны формировать поддерево в нумерации Ли Чена.
1
3
1 2
2 3
1
1
1
2
2
1
A 1
B 2
C 1
2
6
1 2
1 3
1 4
4 5
4 6
4
1 3 4 5
3
3 5 2
3
6
1 2
1 3
1 4
4 5
4 6
3
1 2 3
3
4 1 6
5
B 2
C 1
A 1
C -1
В первом примере $$$[2, 3, 1]$$$ является скрытой перестановкой Ли Чена, а во втором примере его скрытой перестановкой является $$$[5, 3, 2, 4, 1, 6]$$$.
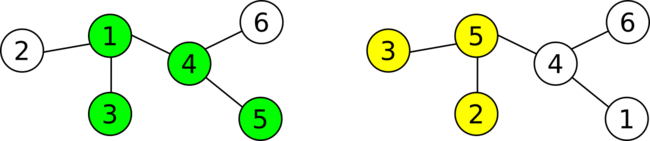
В первом примере есть дерево из трех вершин. Сверху расположено дерево в вашей нумерации и поддерево, которое вы выбрали, а внизу расположено дерево пронумерованное Ли Ченом и его поддерево:

Первым вопросом вы можете попросить Андрея посмотреть на вершину $$$1$$$ в вашей нумерации и сказать её в нумерации Ли Чена. Андрей ответит $$$2$$$. В этот момент вы знаете, что оба ваших поддеревья содержат одну и ту же вершину (то есть вершину $$$1$$$, в соответствии с вашей нумерацией), значит вы могли бы вывести «C 1» и закончить. Однако, вы просите Андрея посмотреть, как обозначена вершина $$$2$$$ в нумерации Ли Чена и сказать её номер в вашей нумерации. Андрей ответит $$$1$$$ (этот вопрос был показан по единственной причине — показать вам как задавать вопросы).
Во втором примере есть два тестовых случая. Первый выглядит так же, как и пример в условии:
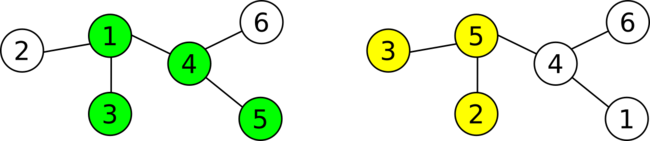
Сначала мы спросим «B 2», и Андрей ответит $$$3$$$. В таком случае, мы знаем, что $$$3$$$ является общей вершиной, и более того, любое поддерево с размером $$$3$$$, которое имеет вершину $$$3$$$, так же будет содержать вершину $$$1$$$, то есть мы может вывести либо "C 1", либо "C 3".
Во втором тестовом случае второго примера:
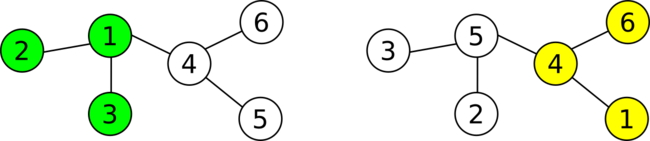
В таком случае, вы знаете что есть только одно поддерево с размером $$$3$$$, которое не содержит вершину $$$1$$$, — это $$$4,5,6$$$. Вы спрашиваете Андрея номер вершины $$$1$$$ в нумерации Ли Чена. Он отвечает $$$5$$$. В таком случае, вы знаете, что поддерево Ли Чена не содержит $$$1$$$, значит его поддерево должно содержать $$$4,5,6$$$ (в его нумерации), по этому два поддерева не имеют общих вершин.
| Название |
|---|