| Codeforces Round 509 (Div. 2) |
|---|
| Закончено |
Монокарп нарисовал дерево (неориентированный связный ацикличный граф) и пронумеровал его вершины. Все номера вершин — различные числа от $$$1$$$ до $$$n$$$. Для каждого ребра $$$e$$$ этого дерева он записал два числа: максимальные номера вершин в каждой компоненте, на которые распалось бы дерево, если бы он удалил ребро $$$e$$$ (и только его).
Монокарп дал вам список из $$$n - 1$$$ пар чисел. По этому списку он просит вас определить, существует ли дерево, для которого мог быть записан именно такой список пар, и если оно существует, предоставить пример.
В первой строке содержится одно число $$$n$$$ ($$$2 \le n \le 1\,000$$$) — количество вершин в дереве.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \le a_i < b_i \le n$$$) — максимумы в тех компонентах, на которые распадается дерево при удалении $$$i$$$-го ребра.
Если дерево, для которого мог быть получен данный список пар, не существует, выведите «NO» (без кавычек).
Иначе в первой строке выведите «YES» (без кавычек), после чего выведите $$$n - 1$$$ строку с описанием рёбер. В каждой из этих $$$n - 1$$$ строк должны быть записаны два числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$) — номера вершин, соединяемых очередным ребром.
Обратите внимание: несмотря на то, что рёбра пронумерованы, ваш ответ будет засчитан как правильный, если по вашему дереву будет получен список из тех же пар чисел, расположенных в другом порядке. Это значит, что вы можете выводить ребра в любом порядке.
4
3 4
1 4
3 4
YES
1 3
3 2
2 4
3
1 3
1 3
NO
3
1 2
2 3
NO
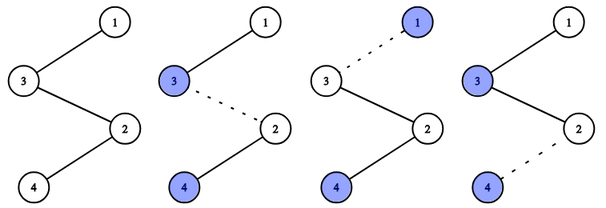
Одно из подходящих деревьев для первого примера. Пунктирные линии показывают ребра, при удалении которых получаются соответствующие пары.
| Название |
|---|




